
Uvod v rekurzivno delovanje na Javi
Rekurzivna funkcija je tista, ki sebe pokliče enkrat ali večkrat. Rekurzivna funkcija se uporablja v situacijah, ko je treba vedno znova izvajati isti niz operacij, dokler rezultat ni dosežen. Izvede več iteracij, težava pa z vsako ponovitvijo postane preprostejša.
Med pisanjem rekurzivne funkcije je treba vedno določiti osnovno mejo, kar povzroči napako prelivanja sklada. Kopček je pomnilniško območje, rezervirano za vzdrževanje priklicev metode. Napaka je v tem, da se funkcija začne izvajati nenehno, saj ne bo mogla najti omejevalnega stanja in s tem končno izčrpati dodeljenega pomnilnika. Da preprečimo prelivanje stack, določimo nekatere osnovne pogoje s pomočjo stavkov "if … else" (ali kakršnih koli drugih pogojnih stavkov), zaradi česar se funkcija rekurzije ustavi takoj, ko se zahtevano izračunavanje zaključi.
Vrste rekurzije na Javi
Na Javi obstajata dve vrsti rekurzije. To so:
1. Neposredna rekurzija
Sintaksa:
Tu funkcija 1 sam sebe kliče nenehno, torej je rekurzivna funkcija.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Primer
Faktor številke je primer neposredne rekurzije. Osnovno načelo rekurzije je reševanje zapletenega problema z delitvijo na manjše. Na primer, v primeru faktororialnih števil izračunamo faktororial "i", če poznamo njegovo faktorje "i-1".
Koda:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Izhod:

2. Posredna / medsebojna rekurzija
Funkcija1, ki pokliče drugo funkcijo2, ki v zameno kliče funkcijo1 neposredno ali posredno, se imenuje indirektna rekurzivna funkcija.
Sintaksa:
Razmislimo o dveh funkcijah, imenovanih function1 () in function2 (). Tukaj funkcija 1 kliče funkcijo2 in funkcija2 kliče funkcijo1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Primer
Če želite prikazati indirektno rekurzijo, vzamemo naslednji program, s katerim ugotovimo, ali je določena številka iz nekega vnosa enaka ali neparna.
Koda:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Izhod:
Primeri rekurzije na Javi
Tu je še nekaj primerov za reševanje težav z metodo rekurzije.
Primer # 1 - Fibonaccijeva zaporedje
Niz številk „n“ naj bi bil v Fibonaccijevem zaporedju, če je število3 = število1 + število2, tj. Vsako število je vsota njegovih prejšnjih dveh števil. Zato se zaporedje vedno začne s prvima dvema števkama, kot sta 0 in 1. Tretja številka je vsota 0 in 1, kar ima za posledico 1, četrta številka je seštevanje 1 in 1, kar pomeni 2, in zaporedje nadaljuje.
Oglejte si naslednjo kodo na Javi, da ustvarite Fibonaccijevo zaporedje:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Izhod:

Tu sta prvi dve številki inicializirani na 0 in 1 in natisnjeni. Spremenljivke „num1“, „num2“ in „num3“ se uporabljajo za ustvarjanje zahtevanega zaporedja. Spremenljivko „num3“ dobimo z dodajanjem „num1“ in „num2“, številke pa se s premikanjem, kot je prikazano v kodi, premaknejo za en položaj v levo. Tu se rekurzivno imenuje funkcija "Fibonaccije" in ob vsaki ponovitvi se vrednost "n" zmanjša za 1. Torej rekurzija izstopi takoj, ko "n" doseže vrednost 0.
Primer # 2 - Hanojski stolp
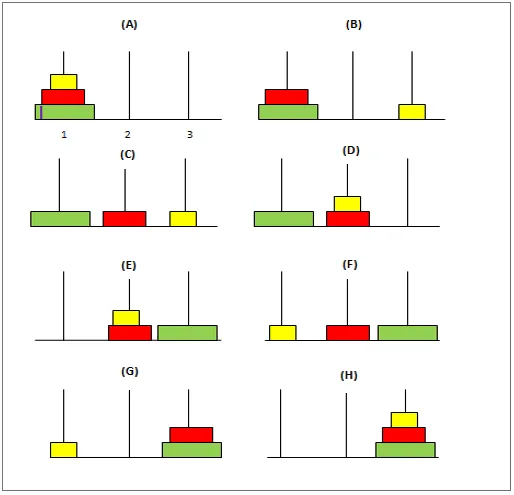
To je klasična matematična težava, ki ima 3 pola in "n" število diskov različnih velikosti. Uganka je naslednja:
Na začetku bo prvi drog postavljen tako, da bo največji disk od vseh na dnu, najmanjši pa na vrhu droga. Cilj je, da se ti diski premikajo s prvega na tretji pol, tako da ostanejo diski v istem položaju kot v prvem. Sledi nekaj pogojev, ki jih morate upoštevati pri premikanju teh diskov:
1. Hkrati je treba premakniti samo en disk.
2. V tem primeru namestitev večjega diska čez manjšega ni dovoljena.
3. Drugi (srednji) drog se lahko uporablja za posredovanje med prenosom plošč iz prvega na drugi pol.
Sledi koda Java, ki jo lahko uporabimo za reševanje uganke:
Koda:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Izhod:
Tu spremenljivka "štetje" predstavlja število uporabljenih diskov. Funkcija "stolp" je rekurzivna funkcija, ki se uporablja za premikanje diskov s palice 1 na palico 3. Preprosto rešitev te težave lahko zagotovite tako, da najprej preučite 2 diska.
- Najprej začnemo s premikanjem diska1 s palice 1 na palico 2.
- Nato premaknemo disk2 na palico 3.
- Končno zaključimo s premikanjem diska1 na palico 3, ki izpolnjuje zahtevano rešitev.
To isto načelo velja za „n“ število diskov s premikanjem (n-1) diska s palice 1 na 2 in po podobnih korakih kot zgoraj.
Prednosti rekurzije na Javi
- Kodo je enostavno napisati in vzdrževati.
- Najboljša metoda za iskanje rezultatov, kjer je potrebno veliko število ponovitev.
Slabosti rekurzije na Javi
- Rekurzivne funkcije uporabljajo več pomnilnika. To je zato, ker se vsakič pokliče rekurzivna funkcija; dodelitev pomnilnika se na novo opravi za spremenljivke na nizu. Ko se vrnejo spremenljive vrednosti, se sprosti dodelitev pomnilnika.
- Ta postopek dodeljevanja pomnilnika traja več časa, zato je izvajanje običajno počasno.
Zaključek
Rekurzivne funkcije so relativno enostavnejše za kodiranje, vendar tudi niso tako učinkovite v primerjavi z drugimi obstoječimi metodami. Zato se večinoma uporabljajo v primerih, ko je čas, namenjen razvoju, krajši in tudi v težavah lahko opazimo pomemben vzorec.
Priporočeni članki
To je vodnik za rekurzijo na Javi. Tukaj razpravljamo o vrstah rekurzije na Javi in njenih različnih primerih s prednostmi in slabostmi. Če želite izvedeti več, si oglejte tudi naslednje članke -
- JScrollPane v Javi
- Funkcije matematike na Javi
- Funkcije matematike na Javi
- Konstruktor v Javi
- Rekurzivna funkcija v Pythonu
- Faktorski program v JavaScript