
Formula efektivne obrestne mere (vsebina)
- Formula
- Primeri
- Kalkulator
Kakšna je formula efektivne obrestne mere?
Izraz "efektivna obrestna mera" se nanaša na dejanski letni donos naložbe, ki je dosežen zaradi rezultata združevanja v časovnem obdobju. Nasprotno pa se z vidika posojilojemalca efektivna obrestna mera lahko šteje za resnične stroške izposoje. Znana je tudi kot efektivna letna donosnost ali letna enakovredna stopnja. Formulo za učinkovito obrestno mero je mogoče izpeljati na podlagi navedene obrestne mere in števila zamudnih obdobij na leto. Matematično je predstavljeno kot
Effective Interest Rate = (1 + i/n) n – 1
kje,
- i = Navedena obrestna mera
- n = Število sestavljenih obdobij na leto
Primeri formule efektivne obrestne mere (s predlogo Excel)
Vzemimo primer, da bolje razumemo izračun efektivne obrestne mere.
Predlogo Excel-ove formule za efektivno obrestno mero lahko prenesete tukaj - Predloga formule efektivne obrestne mereFormula efektivne obrestne mere - primer # 1
Vzemimo primer naložbe z navedeno 10-odstotno obrestno mero. Izračunajte efektivno obrestno mero, če se naložba sestavi dvakrat letno.
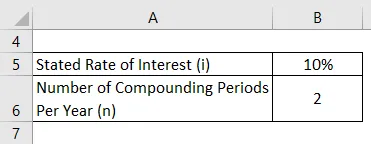
Rešitev:
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1

- Efektivna obrestna mera = (1 + 10% / 2) 2 - 1
- Efektivna obrestna mera = 10, 25%
Zato znaša efektivna obrestna mera za naloženo naložbo 10, 25%.
Formula efektivne obrestne mere - primer # 2
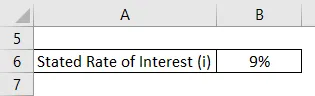
Vzemimo primer Johna, ki je zainteresiran za naložbo obveznice, ki ponuja navedeno 9-odstotno obrestno mero. Vendar pa je narava sestavljenosti drugačna in John ni prepričan, katero mešanje bo prineslo največ donosa. Izračunajte efektivno obrestno mero in pomagajte Janezu, da se uspešno odloči za naslednje obdobje zapletov:
- Letna
- Polletno
- Četrtletno
- Mesečno
- Vsakodnevno
Letna
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1
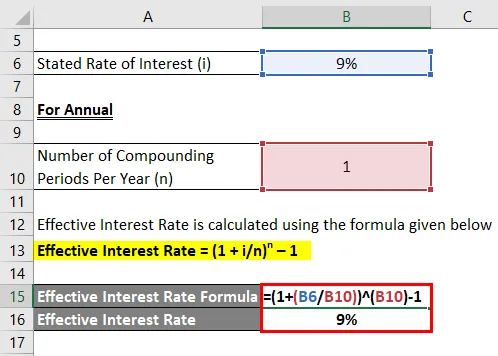
- Efektivna obrestna mera = (1 + 9% / 1) 1 - 1
- Efektivna obrestna mera = 9%
Polletno
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1
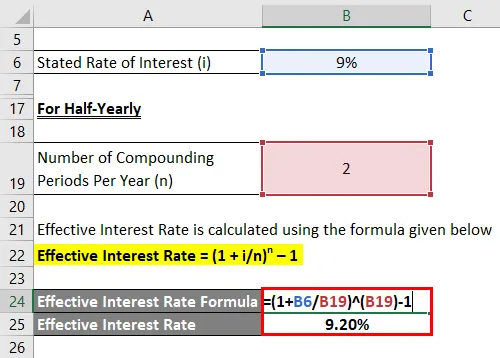
- Efektivna obrestna mera = (1 + 9% / 2) 2 - 1
- Efektivna obrestna mera = 9, 20%
Četrtletno
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1
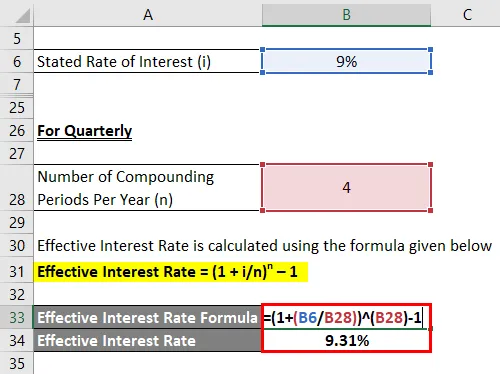
- Efektivna obrestna mera = (1 + 9% / 4) 4 - 1
- Efektivna obrestna mera = 9, 31%
Mesečno
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1
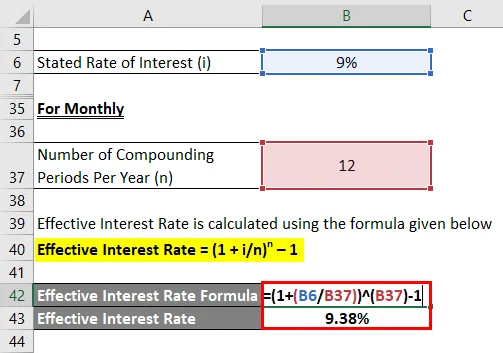
- Efektivna obrestna mera = (1 + 9% / 12) 12 - 1
- Efektivna obrestna mera = 9, 38%
Vsakodnevno
Efektivna obrestna mera se izračuna po spodnji formuli
Efektivna obrestna mera = (1 + i / n) n - 1

- Efektivna obrestna mera = (1 + 9% / 365) 365 - 1
- Efektivna obrestna mera = 9, 42%
Zato je jasno razvidno, da se letni pridelek povečuje s povečanjem števila mešanic, ki se zgodijo na leto. Možnost dnevnega mešanja bo ponudila Johnu najboljši donos (efektivna 9, 38-odstotna obrestna mera 9-odstotna).
Pojasnilo
Formulo učinkovite obrestne mere je mogoče izvesti z naslednjimi koraki:
1. korak: Najprej določite navedeno obrestno mero za naložbo, ki je običajno navedena v investicijskem dokumentu. Označen je z „i“.
Korak 2: Nato določite število obdobij v enem letu in ga označite s "n". Običajno sestavljajo četrtletno, polletno in letno, kar pomeni število mešanic na leto 4, 2 in 1.
Korak 3: Končno lahko formulo učinkovite obrestne mere dobimo z uporabo navedene obrestne mere (korak 1) in številnih obdobij sestavljanja na leto (korak 2), kot je prikazano spodaj.
Efektivna obrestna mera = (1 + i / n) n - 1
Ustreznost in uporaba formule efektivne obrestne mere
Pomembno je razumeti koncept učinkovite obrestne mere, ker je za vlagatelja ali drugega finančnega uporabnika ključna metrika. Vlagatelji ponavadi uporabljajo efektivno obrestno mero, saj gre za dejanski donos, pridobljen iz naložbe. Tako vlagatelji dajejo večji poudarek na število mešanic na leto, saj večje število mešanic pomeni večji donos. Po drugi strani se perspektiva spremeni za posojilojemalca, ki si prizadeva za manjše število poravnav na leto, saj bi ohranil nizke odhodke za obresti in prinesel boljšo dobičkonosnost.
Koncept efektivne obrestne mere je zelo odvisen od števila združevanj, ki se zgodijo v letu, končno pa višji donos ali sčasoma višja odkupna vrednost ob zapadlosti. Običajno se efektivna letna stopnja povečuje s povečanjem števila mešanic na leto. Čeprav je mogoče sestaviti neskončno večkrat, ne pozabite, da obstaja učinek mešanja, ki presega to, da se pojav preneha dogajati. Ta vrsta združevanja je znana kot neprekinjeno združevanje, za katero je efektivna obrestna mera izražena kot - e, i. Je navedena obrestna mera in je neodvisna od obdobja združevanja.
Kalkulator formule efektivne obrestne mere
Uporabite lahko naslednji kalkulator formule efektivne obrestne mere
| jaz | |
| n | |
| Efektivna obrestna mera | |
| Efektivna obrestna mera = | (1 + i / n) n –1 |
| = | (1 + 0/0) 0 -1 = 0 |
Priporočeni članki
To je vodnik po formuli učinkovite obrestne mere. Tukaj razpravljamo, kako izračunati efektivno obrestno mero skupaj s praktičnimi primeri. Ponujamo vam tudi kalkulator učinkovite obrestne mere s prenosljivo predlogo Excela. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Formula za mesečne sestavljene obresti
- Kako izračunati nominalno obrestno mero?
- Primeri odhodkov za obresti
- Izračun nominalne formule BDP
- Obresti v primerjavi z dividendami | Top 8 ključnih razlik, ki bi jih morali vedeti