Razlika med linearno regresijo in logistično regresijo
Naslednji članek Linear Regression vs Logistic Regression ponuja najpomembnejše razlike med obema, a preden bomo videli, kaj pomeni regresija?
Regresija
Regresija je v osnovi statistični ukrep za določitev jakosti povezave med eno odvisno spremenljivko, tj. Izhodom Y in vrsto drugih neodvisnih spremenljivk, tj. X 1, X 2 in tako naprej. Regresijska analiza se v osnovi uporablja za napovedovanje in napovedovanje.
Kaj je linearna regresija?
Linearna regresija je algoritem, ki temelji na nadzorovanem učnem področju strojnega učenja. Podeduje linearno razmerje med vhodnimi spremenljivkami in enojno izhodno spremenljivko, kjer je izhodna spremenljivka neprekinjena. Uporablja se za napovedovanje vrednosti izhodne vrednosti, recimo Y iz vhodov, recimo X. Ko štejemo samo en vhod, se imenuje preprosta linearna regresija.
Lahko ga razvrstimo v dve glavni kategoriji:
1. Enostavna regresija
Osnove delovanja: glavni cilj je najti enačbo ravne črte, ki najbolje ustreza vzorčenim podatkom. Ta enačba algebraično opisuje odnos med obema spremenljivkama. Najbolj primerna ravna črta se imenuje regresijska linija.
Y = β 0 + β 1 X
Kje,
β predstavlja lastnosti
β 0 predstavlja prestrezanje
β 1 predstavlja koeficient lastnosti X
2. Multivarijantna regresija
Uporablja se za napovedovanje povezave med več neodvisno spremenljivko in eno odvisno spremenljivko. Regresija z več kot dvema neodvisnima spremenljivkama temelji na ustrezni obliki v konstelacijo podatkov na večdimenzionalnem grafu. Oblika regresije mora biti taka, da zmanjša razdaljo oblike od vsake podatkovne točke.
Model linearnega razmerja je mogoče matematično predstaviti kot spodaj:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Kje,
β predstavlja lastnosti
β 0 predstavlja prestrezanje
β 1 predstavlja koeficient lastnosti X 1
β n predstavlja koeficient lastnosti X n
Prednosti in slabosti linearne regresije
Spodaj so navedene prednosti in slabosti:
Prednosti
- Zaradi svoje preprostosti se pogosto uporablja za modeliranje napovedi in sklepov.
- Osredotoča se na analizo podatkov in predobdelavo podatkov. Torej, obravnava različne podatke, ne da bi se trudil s podrobnostmi modela.
Slabosti
- Učinkovito deluje, ko se podatki običajno distribuirajo. Tako je za učinkovito modeliranje treba preprečiti kolinearnost.
Kaj je logistična regresija?
To je oblika regresije, ki omogoča napovedovanje diskretnih spremenljivk z mešanico neprekinjenih in diskretnih napovedovalcev. Rezultat je edinstvena preobrazba odvisnih spremenljivk, ki vpliva ne le na postopek ocenjevanja, temveč tudi na koeficiente neodvisnih spremenljivk. Obravnava isto vprašanje, kot ga ima večkratna regresija, vendar brez distribucijskih predpostavk o napovedovalcih. V logistični regresiji je spremenljivka rezultata binarna. Namen analize je oceniti učinke več pojasnjevalnih spremenljivk, ki so lahko numerične ali kategorične ali oboje.
Vrste logistične regresije
Spodaj sta dve vrsti logistične regresije:
1. Binarna logistična regresija
Uporablja se, kadar je odvisna spremenljivka dihotomna, tj. Kot drevo z dvema vejama. Uporablja se, kadar je odvisna spremenljivka neparametrična.
Uporablja se kdaj
- Če ni linearnosti
- Obstajata le dve ravni odvisne spremenljivke.
- Če je multivariatna normalnost dvomljiva.
2. Multinomična logistična regresija
Multinomična logistična regresijska analiza zahteva, da so neodvisne spremenljivke metrične ali dihotomne. Za neodvisne spremenljivke ne daje nobenih predpostavk o linearnosti, normalnosti in homogenosti variance.
Uporablja se, kadar ima odvisna spremenljivka več kot dve kategoriji. Uporablja se za analizo razmerij med ne metrično odvisno spremenljivko in metričnimi ali dihotomnimi neodvisnimi spremenljivkami, nato pa primerja več skupin s kombinacijo binarnih logističnih regresij. Na koncu poda niz koeficientov za vsako od obeh primerjav. Koeficienti za referenčno skupino so vsi ničli. Končno napovedovanje poteka na podlagi najvišje rezultatske verjetnosti.
Prednost logistične regresije: Je zelo učinkovita in široko uporabljena tehnika, saj ne potrebuje veliko računskih virov in ne potrebuje nobene prilagoditve.
Pomanjkljivost logistične regresije: ni ga mogoče uporabiti za reševanje nelinearnih problemov.
Primerjava med posameznimi linijami med linearno regresijo in logistično regresijo (Infographics)
Spodaj je zgornjih 6 razlik med Linear Regression in Logistic Regression 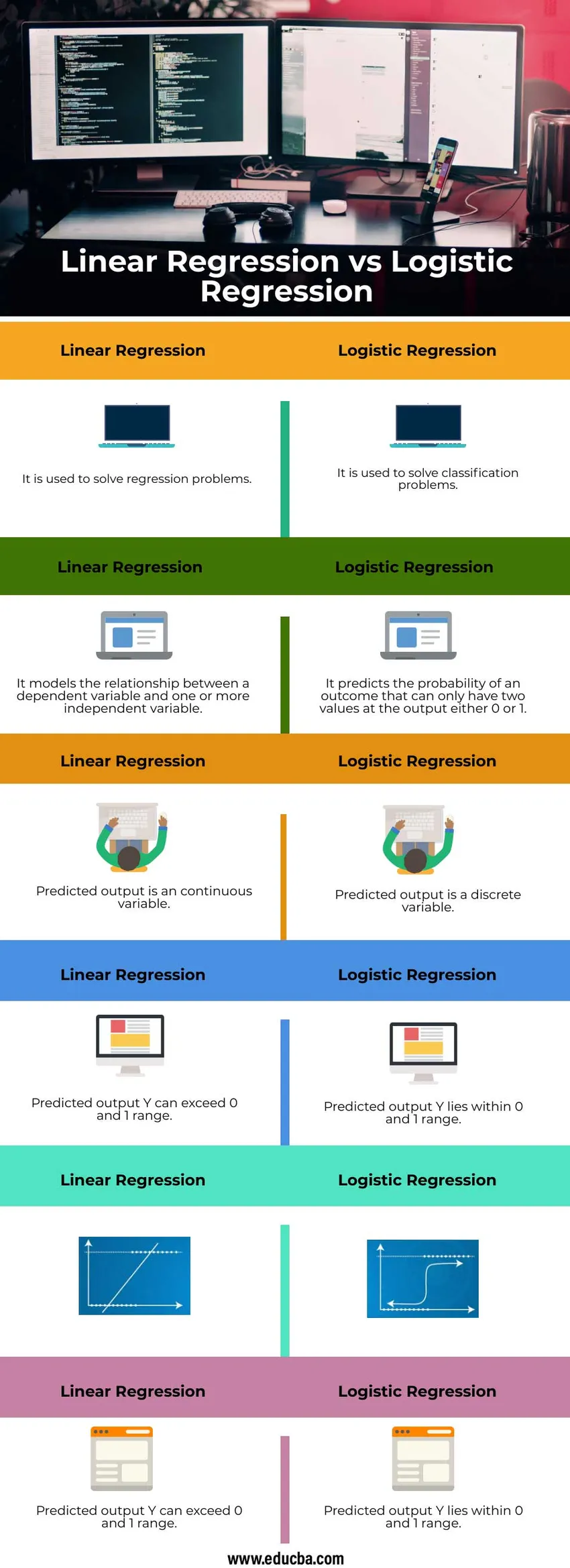
Ključna razlika med linearno regresijo in logistično regresijo
Pogovorimo se o nekaterih glavnih ključnih razlikah med Linearno regresijo in logistično regresijo
Linearna regresija
- Gre za linearni pristop
- Uporablja ravno črto
- Ne more sprejeti kategoričnih spremenljivk
- Ignorirati mora opazovanja z manjkajočimi vrednostmi numerične neodvisne spremenljivke
- Izhod Y je podan kot
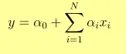
- 1 enotno povečanje x poveča Y za α
Prijave
- Napovedovanje cene izdelka
- Napovedovanje rezultata na tekmi
Logistična regresija
- Gre za statistični pristop
- Uporablja sigmoidno funkcijo
- Lahko sprejme kategorične spremenljivke
- Sprejema lahko odločitve, tudi če so prisotna opažanja z manjkajočimi vrednostmi
- Izhod Y je podan kot, pri čemer je z dan kot
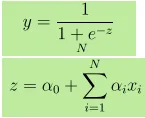
- 1 enotno povečanje x poveča Y z ločljivostmi od α
- Če je P verjetnost dogodka, potem je (1-P) verjetnost, da se ne bo zgodil. Kvote uspeha = P / 1-P
Prijave
- Napovedovanje, ali bo danes deževalo ali ne.
- Napovedovanje, ali je e-pošta nezaželena ali ne.
Primerjalna tabela linearne regresije in logistične regresije
Pogovorimo se o zgornji primerjavi med Linear Regression in Logistic Regression
|
Linearna regresija |
Logistična regresija |
| Uporablja se za reševanje regresijskih težav | Uporablja se za reševanje težav s klasifikacijo |
| Modelira razmerje med odvisno spremenljivko in eno ali več neodvisnimi spremenljivkami | Napoveduje verjetnost izida, ki ima lahko na izhodu le dve vrednosti bodisi 0 bodisi 1 |
| Predvideni izhod je zvezna spremenljivka | Predvideni izhod je diskretna spremenljivka |
| Predvideni izhod Y lahko presega območje 0 in 1 | Predvideni izhod Y leži v območju 0 in 1 |
 | 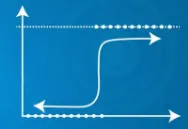 |
| Predvideni izhod Y lahko presega območje 0 in 1 | Napovedani izhod |
Zaključek
Če funkcije ne prispevajo k napovedovanju ali so med seboj zelo povezane, potem modelu doda hrup. Torej je treba odstraniti lastnosti, ki ne prispevajo dovolj k modelu. Če so neodvisne spremenljivke zelo povezane, lahko povzroči problem multikolinearnosti, ki ga je mogoče rešiti z izvajanjem ločenih modelov z vsako neodvisno spremenljivko.
Priporočeni članki
To je vodnik za Linear Regression vs Logistic Regression. Tukaj razpravljamo o ključnih razlikah Linear Regression vs Logistic Regress z infografiko in primerjalno tabelo. Za več informacij si lahko ogledate tudi naslednje članke -
- Data Science vs vizualizacija podatkov
- Strojno učenje proti nevronski mreži
- Nadzorovano učenje vs poglobljeno učenje
- Logistična regresija v R