
Uvod v matematične funkcije Pythona
V pythonu se z matematičnim modulom python lotevajo vseh matematičnih potreb. ta modul je v veliki meri razvrščen z različnimi matematičnimi funkcionalnostmi, vgrajenimi vanj. V matematičnem modulu so vključene skoraj vse priljubljene matematične funkcije. To je takoj na voljo standardni modul v pythonu. To je mogoče uvoziti s stavkom uvoz matematike.
Različne matematične funkcije v Pythonu
Spodaj so podrobno opisane vse ključne matematične funkcije,
1. Konstante
V primeru matematične konstante je vrednost za to konstanto predstavljena z nedvoumno definicijo, te definicije so v nekaterih primerih predstavljene s kakršnimi koli posebnimi simboli ali s kakšnimi znanimi imeni matematikov ali s katerim koli drugim priljubljenim sredstvom. Konstante se pojavljajo na številnih področjih matematike s pomočjo konstant, kot sta π in e, ki se dogajajo v različnih okoliščinah, kot so teorija števil, geometrija in preračun.
Pomen stalnice, ki se poraja »naravno« in je nenehno »zanimiva«, je v določenem času potreben material, zato so številne matematične konstante pomembnejše zaradi kronoloških razlogov kot zaradi svojih temeljnih matematičnih interesov. Bolj všečne konstante so bile proučene skozi stoletja in izračunane na veliko decimalnih mest.
| Konstante | Opis |
| pi | vrne 3.141592 |
| E | vrne 0, 718282 |
| nan | Ne številka |
| inf | neskončno |
Primer:
import math
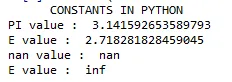
print( "CONSTANTS IN PYTHON")
print(" PI value : ", math.pi)
print(" E value : ", math.e)
print(" nan value : ", math.nan)
print(" E value : ", math.inf)
Izhod:
2. Logaritmične funkcije
Inverzacija za eksponentacijo se imenuje kot logaritem. Za katero koli število x, da bi določili njegovo logaritmsko vrednost, se izračuna eksponent drugega fiksnega števila z bazo b. V bolj neposrednem primeru logaritem izračuna ali šteje številčne pojavitve istega faktorja pri večkratnem množenju;
Na primer: 1000 = 10 × 10 × 10 = 103, potem je "logaritem do osnove 10" 1000 enak 3. Logaritem x do osnove b je označen kot logb (x).
Po drugi strani pa eksponent števila pomeni, kolikokrat se število uporabi v množitvenem faktorju.
Primer: 82 = 8 × 8 = 64
Z besedami lahko predstavitev 82 imenujemo "8 na moč 2" ali preprosto kot "8 na kvadrat". Po drugi strani pa eksponent števila pomeni, kolikokrat se število uporabi v množitvenem faktorju.
| Funkcija | Opis |
| exp (x) | Vrne e ** x |
| expm1 (x) | Vrne e ** x - 1 |
| dnevnik (x (, osnova)) | x v osnovni logaritem se vrne |
| log1p (x) | Base1 logaritem vrednosti x se vrne |
| log2 (x) | Base2 logaritem vrednosti x se vrne |
| log10 (x) | Base10 logaritem vrednosti x se vrne |
| Pow (x, y) | Vrne x, dvignjeno na moč y |
| sqrt (x) | Vrnjena je kvadratna vrednost korena za x |
Primer:
import math
#variable declaration and assignation
Number_1 = 1
Number_2 = 2
Number_3 = 3
Number_4 = 4
# Applying exp() function
print(" EXPONENT VALUE ")
print(" Exponent value: ", math.exp(Number_1))
print(" \n ")
# Applying Base1 logarithm function
print(" BASE1 LOGARITHM " )
print(" BASE1 LOGARITHM VALUE of 2 : ", math.log1p(Number_2))
print(" \n " )
# Applying Base2 logarithm function
print(" BASE2 LOGARITHM " )
print(" BASE2 LOGARITHM VALUE of 2 : ", math.log2(Number_2))
print(" \n " )
# Applying Base10 logarithm function
print(" BASE10 LOGARITHM " )
print(" BASE10 LOGARITHM VALUE of 2 : ", math.log10(Number_2))
print(" \n " )
# Applying x to power of Y
print(" X^Y" )
print(" X^Y Value : ", math.pow(Number_3, Number_4))
print(" \n " )
# Applying square root determination
print(" SQUARE ROOT " )
print(" SQUARE ROOT of 4 : ", math.sqrt(Number_4))
print(" \n " )
Izhod:

3. Številske funkcije
Številske funkcije omogočajo izračun vseh matematičnih zaznav.
| Konstante | Opis |
| strop (x) | Vrne se najmanjše celo število, ki je zelo veliko ali enako vrednosti x |
| copysign (x, y) | Z znakom y se vrne vrednost za x |
| Fabs (x) | absolutna vrednost za x se vrne |
| faktororial (x) | faktorska vrednost x se vrne |
| nadstropje (x) | vrne se največje celo število, ki je zelo veliko ali enako vrednosti x |
| fmod (x, y) | se vrne preostali delitev x z y vrednostjo |
| frexp (x) | Vrne mantiso in eksponent x kot para (m, e) |
| fsum (iterable) | Vrne natančno vsoto vrednosti s plavajočo vejico v ponovljivi |
| neskončno (x) | če x ni neskončnost ali Nan, se vrne logična vrednost true |
| isinf (x) | če ima x pozitivno ali negativno neskončnost, se vrne true |
| Isnan (x) | Vrne True, če je x NaN |
| gcd (x, y) | za vrednosti x in y se vrne največ skupne vrednosti delitelja |
| preostanek (x, y) | Poiščite preostanek, potem ko x delite z y. |
Primer:
import math
#variable declaration and assignation
Number_1 = 10.5
Number_2 = 20
Number_3 = -30
Number_4 = -40.24566
Number_5 = 50
Number_6 = 60.94556
Number_7 = 70
Number_8 = 80
# Applying Ceil() function
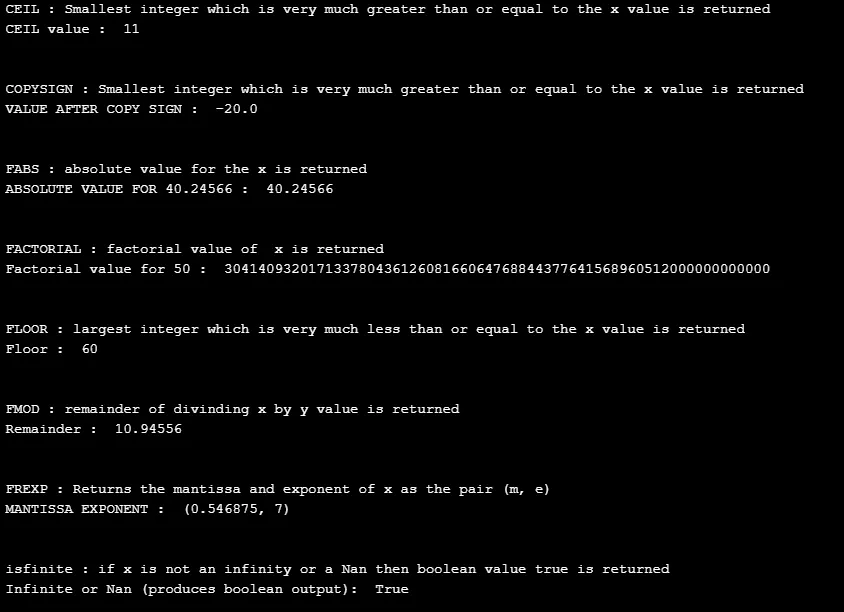
print( " CEIL : Smallest integer which is very much greater than or equal to the x value is returned ")
print( " CEIL value : ", math.ceil(Number_1))
print( " \n " )
# Applying Copysign() function
print( " COPYSIGN : Smallest integer which is very much greater than or equal to the x value is returned ")
Temp_var1 = math.copysign(Number_2, Number_3)
print(" VALUE AFTER COPY SIGN : ", Temp_var1)
print(" \n ")
# Applying fabs() function
print( " FABS : absolute value for the x is returned ")
print(" ABSOLUTE VALUE FOR 40.24566 : ", math.fabs(Number_4))
print(" \n ")
# Applying Factorial() function
print(" FACTORIAL : factorial value of x is returned ")
print(" Factorial value for 50 : ", math.factorial(Number_5))
print(" \n ")
# Applying Floor() function
print(" FLOOR : largest integer which is very much less than or equal to the x value is returned " )
print(" Floor : ", math.floor(Number_6))
print(" \n ")
# Applying Fmod() function
print(" FMOD : remainder of divinding x by y value is returned ")
print(" Remainder : ", math.fmod(Number_6, Number_5))
print(" \n ")
# Applying Frexp() function
print( " FREXP : Returns the mantissa and exponent of x as the pair (m, e) " )
print(" MANTISSA EXPONENT : ", math.frexp(Number_7))
print( " \n " )
# Applying isfinite() function
print(" isfinite : if x is not an infinity or a Nan then boolean value true is returned ")
print(" Infinite or Nan (produces boolean output): ", math.isfinite(Number_8))
print(" \n ")
Izhod:
4. Trigonometrične funkcije
V matematiki so trigonometrične funkcije funkcije, ki se uporabljajo za prikazovanje vidika pravokotnega trikotnika v dveh stranskih dolžinah. imajo zelo velik nabor aplikacij v znanostih, ki so sorodne geometriji, kot so trdna mehanika, nebesna mehanika, navigacija, veliko drugih. Šteje se za preproste periodične funkcije in splošno znano predstavlja periodične pojave, od začetka do konca Fourierove analize.
| funkcijo | Opis |
| greh (x) | določena je sinusna vrednost x v radianih |
| cos (x) | treba je določiti kosinusno vrednost x v radianih |
| porjavelost (x) | Določiti je treba tangentno vrednost x v radianih |
| stopinj (x) | pretvorba radiana v stopinjo |
| radian (x) | stopnjo pretvorbe radiana |
Primer:
import math
print(" \n ")
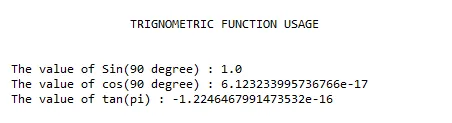
print(" TRIGNOMETRIC FUNCTION USAGE " )
print(" \n ")
print(' The value of Sin(90 degree) : ' + str(math.sin(math.radians(90))))
print(' The value of cos(90 degree) : ' + str(math.cos(math.radians(90))))
print(' The value of tan(pi) : ' + str(math.tan(math.pi)))
print(" \n ")
Izhod:
Zaključek - Math funkcije v Pythonu
Tako kot mnogi drugi programski jeziki tudi Python ponuja zelo raznolik nabor matematičnih funkcij, zaradi česar v programskem prizorišču močno implicira programski jezik na visoki ravni.
Priporočeni članki
To je vodnik za Math funkcije v Pythonu. Tukaj s primeri obravnavamo različne matematične funkcije v Pythonu. Ogledate si lahko tudi druge naše predlagane članke -
- Seznam operacij v Pythonu
- Factorial v Pythonu
- Niz nizov v Pythonu
- Operacije datotek Python
- Funkcije matematike v C # z lastnostmi
- Python Set
- Uvod v matematične funkcije v C
- Kvadratni koren v PHP
- Niz nizov v JavaScript