
Uvod v Fibonaccijevo serijo v Pythonu
Fibonaccijeva serija v Pythonu, to se imenuje niz števil, kjer je naslednje število vsota sedanjih dveh števil.
Primer:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. tako naprej
Torej, tukaj 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 in tako naprej.
Če pogledamo zgoraj, bi človek dobil določeno predstavo o tem, o čem govorimo.
Vendar v smislu matematičnega pravila lahko zapišemo kot:

Kjer je nth število vsota števila na mestih (n-1) in (n-2). Ko gre za implementacijo Fibonaccijeve serije, bi lahko obstajali številni kodni jeziki, s pomočjo katerih bi bilo to mogoče storiti.
Vendar je Python danes zelo razširjen jezik. Oglejmo si izvedbo Fibonaccijeve serije prek Pythona. Preden nadaljujete tukaj, se morate zavedati osnovnih stavkov pogojev, kot so zanka, če-drugače, medtem ko je zanka itd. Če ne, bi bilo super, če ga lahko kdo revidira in nato prevzame prihajajočo vsebino. Tukaj za demo namene uporabljam spyder, ki je IDE za programski jezik python. Za izvedbo programov Python lahko uporabite tudi katere koli prenosne računalnike IDE ali Ipython.
Fibonaccijeva serija v Pythonu
Poglejmo izvedbo Fibonaccijevega števila in serij, ki upoštevata prva dva elementa Fibonacije sta 0 in 1:
Vendar lahko prilagodite funkcijo Fibonaccije glede na vaše zahteve, vendar najprej vidite osnove in postopoma preidete na druge.
Pythonova koda za iskanje n -tega Fibonaccijevega števila
Koda 1:
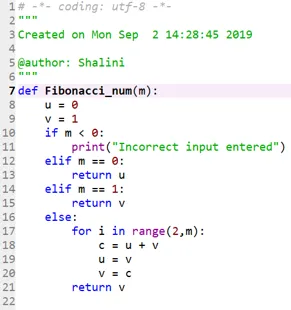
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Koda 2:
Izhod:
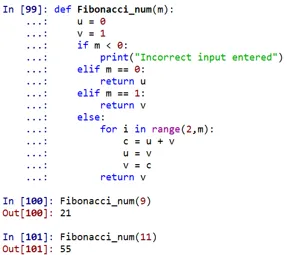
Kot lahko vidimo, bi Fibonaccijeva številka na 9. mestu znašala 21, na 11. mestu pa 55.
- Tu je „Weight_num“ definirana funkcija, ki skrbi za iskanje Fibonaccijevega števila s pomočjo določenih pogojev. To funkcijo lahko pokličete tako, da določite kateri koli položaj.
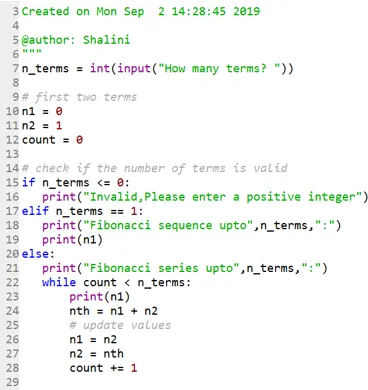
Zdaj pa poglejmo, kako lahko tiskamo serije do omenjenega položaja:
Koda:
Izhod:
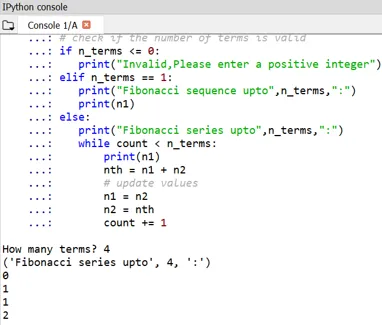
Lahko opazimo, da je začetek Fibonaccijevih števil definiran kot 0 in 1.
- Če želi nekdo določiti svoje lastne izhodiščne pogoje, lahko to stori tudi na enak način s prepletanjem n1 in n2. Tu je primer za to:
Recimo zdaj, da želimo, da so naši začetni izrazi: n1 = 3, n2 = 5
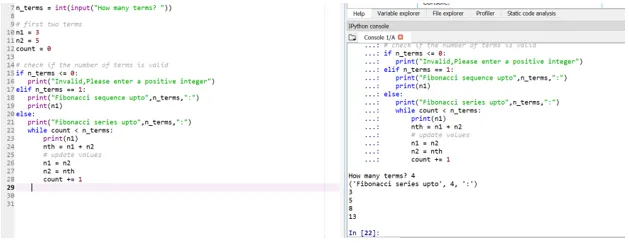
Torej, tukaj bo vaš četrti mandat (uporabniški vnos) določen glede na vaše začetne pogoje.
Metode, s pomočjo katerih je mogoče ustvariti Fibonaccijeve vrste
Spodaj so tri metode, s pomočjo katerih je mogoče ustvariti Fibonaccijeve vrste:
1. Prek generatorjev
Koda:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Izhod:
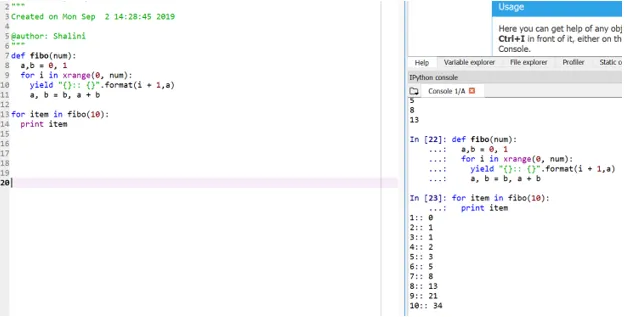
Ta metoda se imenuje "generator", ker je funkcija xrange generator številk med 0 in število, donos pa generator za oblikovani izhod.
Tukaj je, kaj xrange naredi za vas:

Tu je bila Fibonaccijeva serija določena v obliki funkcije, znotraj katere za izhodni položaj skrbi funkcija zanke, xrange in donosnosti.
2. Skozi zanko
Koda:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Izhod:

Kot lahko vidimo, je za tiskanje Fibonaccijeve serije med 0 in 10. uporabljeno preprosto za zanko. Znotraj za zanko so spremenljivkam dodeljene nove vrednosti. U in v sta privzeti začetni vrednosti Fibonaccije, ki sta bili nastavljeni na 0 in 1.
Kar zadeva napredek zanke, je nova vrednost u stara vrednost v, medtem ko je nova vrednost v vsota starih vrednosti u in v. To se nadaljuje do konca vrednosti obsega.
3. Skozi rekurzijo
Koda:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Izhod:
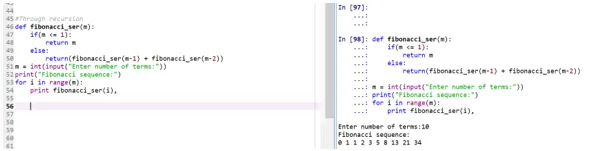
- Funkcija „Weight_ser“ kliče k sebi, da natisne Fibonaccijevo serijo.
- In od tod metoda je dobila ime "rekurzija".
Tukaj sledijo koraki:
- Tu je uporabnik pozvan, naj vnese kraj, do katerega mora biti natisnjena serija Fibonaccije.
- Številka prehaja skozi funkcijo "Weight_ser".
- Pogoj se preveri, če je navedena dolžina manjša od 1 ali ne. Če je odgovor da, je rezultat dan takoj.
- Če pa je dolžina večja od 1, se rekurzivni klici izvedejo na "telo_ser" z argumenti, ki imajo dolžino manjšo od 1 in 2, tj.
- Torej rekurzija daje želeni izhod in ga natisne.
- Torej, na kratko, Razpravljali smo o treh načinih za prikaz Fibonaccijeve serije.
- Skozi zanko, prek generatorjev in prek rekurzije.
Vse tri Python kode so povzete
Spodaj so tri kode pytona:
1. Prek generatorjev
Koda:
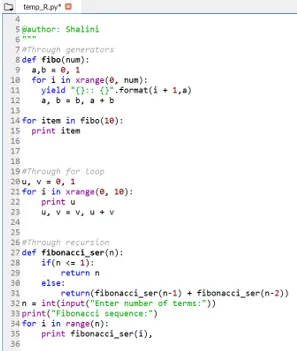
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Skozi zanko
Koda:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Skozi rekurzijo
Koda:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
V nadaljevanju so povzeti vsi postopki, ki jih je treba vaditi, da se dobro oprijete vseh.
Izhod:
Zaključek
Skozi zgornjo vsebino Fibonaccija bi človek dobil kristalno jasno razumevanje Fibonaccijevih števil in serij, specializiranih za pyton. Ko se boste nekoč sprijaznili z logiko serije Fibonaccije, ustvarjanje drugega niza serij, delo z drugimi številkami in z različnimi metodami bo zdaj za vas pravi potez. Logični pristop je edini način, da se pri tem izvrstno odlikuje.
Priporočeni članki
To je vodnik za Fibonaccijeve serije v Pythonu. Tukaj razpravljamo o Fibonaccijevih številkah in serijah, specializiranih za pyton, ustvarjamo še en niz serij, delamo z drugimi številkami in z različnimi metodami. Obiščite lahko tudi druge naše sorodne članke, če želite izvedeti več -
- Generator naključnih števil v Pythonu
- Matematične funkcije v Pythonu
- Factorial v Pythonu
- Inkapsulacija v Pythonu
- Serija Fibonaccije na Javi
- Značilnosti Pythona
- Faktorski program v JavaScript
- Generator naključnih števil v Matlabu
- Generator naključnih števil v C #
- Kapsulacija v JavaScript