Formula efektivne letne stopnje (kazalo)
- Formula
- Primeri
- Kalkulator
Kakšna je efektivna letna formula formule?
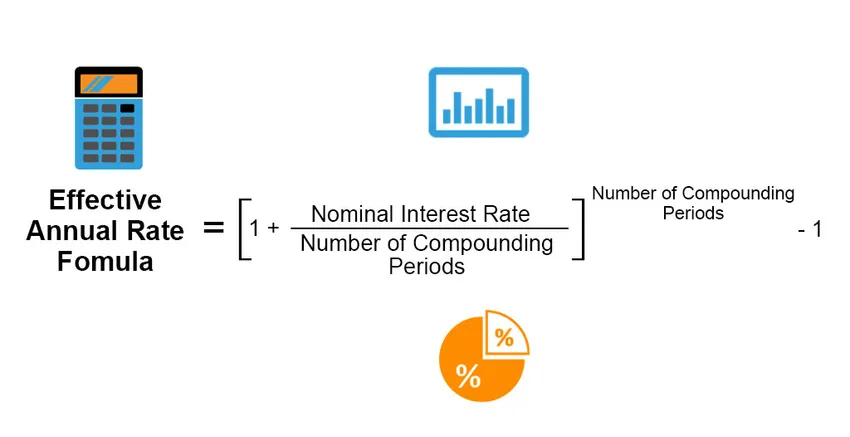
Efektivna letna obrestna mera je dejanska obrestna mera, ki se zasluži ali izplača za naložbo, posojilo ali kateri koli podoben finančni izdelek, in je drugače različna od "nominalne obrestne mere" zaradi obdobja izplačila obresti, sestavljenega iz obrestne mere, skupaj časovno obdobje posojila ali naložbe itd. efektivna letna stopnja se izračuna po naslednji formuli;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Primeri formule učinkovite letne stopnje (s predlogo Excel)
Vzemimo primer, da bolje razumemo izračun efektivne letne stopnje.
Predlogo Excel-ove predloge za efektivno letno obrestno mero lahko prenesete tukaj - Predloga efektivne letne stopnje formule ExcelFormula efektivne letne stopnje - Primer # 1
Recimo, da gospod X vzame osebno posojilo pri banki z obrestno mero 20%, sestavljeno polletno. Z uporabo informacij izračunajte efektivno letno stopnjo.

Rešitev:
Učinkovita letna stopnja se izračuna po spodnji formuli
Efektivna letna stopnja = ((1 + (nominalna obrestna mera / število sestavljenih obdobij)) število stisnjenih obdobij - 1

- Efektivna letna stopnja = ((1 + (20% / 2)) 2) - 1
- Efektivna letna stopnja = 21%
Formula efektivne letne stopnje - Primer # 2
Recimo, da je gospod A vložil 100 dolarjev v depozitno potrdilo, ki izplačuje nominalno letno obrestno mero 10%, sestavljeno na četrtletni osnovi. Izračunajte efektivno letno stopnjo.

Rešitev:
Učinkovita letna stopnja se izračuna po spodnji formuli
Efektivna letna stopnja = ((1 + (nominalna obrestna mera / število sestavljenih obdobij)) število stisnjenih obdobij - 1
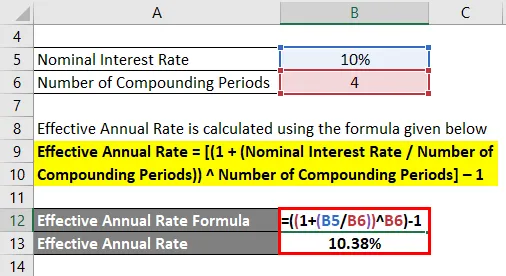
- Efektivna letna stopnja = ((1 + (10% / 4)) 4) - 1
- Efektivna letna stopnja = 10, 38%
Formula efektivne letne stopnje - Primer # 3
Predpostavimo, da naložba v vzajemni sklad prinaša 15, 50% letne obrestne mere kot dobiček, medtem ko P2P Posojilo zasluži 15% letne nominalne obrestne mere, sestavljene mesečno. Torej izračunajte efektivno letno stopnjo za oba primera.

Rešitev:
Učinkovita letna stopnja se izračuna po spodnji formuli
Efektivna letna stopnja = ((1 + (nominalna obrestna mera / število sestavljenih obdobij)) število stisnjenih obdobij - 1
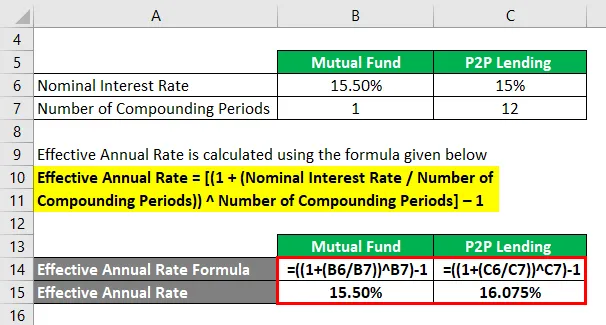
Za vzajemni sklad
- Efektivna letna stopnja = ((1 + (15, 50% / 1)) 1) - 1
- Efektivna letna stopnja = 15, 50%
Za posojanje P2P
- Efektivna letna stopnja = ((1 + (15% / 12)) 12) - 1
- Efektivna letna stopnja = 16.075%
Pojasnilo
Nominalna obrestna mera je navedena stopnja finančnega produkta. V primeru 3 nominalna obrestna mera pri izdelkih naredi vzajemni sklad kot prednostno izbiro naložbe za vlagatelje zaradi 0, 50% višje letne nominalne obrestne mere.
Vendar pa se efektivna letna obrestna mera izračuna tako, da se upošteva nominalna letna obrestna mera in se jo poravna za število določenih obdobij (12, če je združevanje mesečno; 6 če je združevanje dvomesečno; 4 če je četrtletno in 2, če je je polletno), ki se uporablja v obdobju enega leta. V primeru vzajemnega sklada je število obdobij združevanja na leto 1, pri posojilih P2P pa mesečno, zato obstaja 12 obdobij.
Na podlagi formule oz.
Učinkovita letna donosnost = ((1 + (nominalna obrestna mera / število obdobij sestavljanja)) (število obdobij sestavljanja)) - 1
Učinkovita letna donosnost vzajemnega sklada = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
Učinkovita letna donosnost posojila P2P = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Ustreznost in uporaba učinkovite letne formule obrestne mere
Formula efektivne letne obrestne mere se uporablja za razlikovanje dejanske IRR (notranja stopnja donosa) ali letnega donosa za obrestno mero, ki se lahko ali ne sme večkrat sestaviti v določenem obdobju. To bi lahko zelo dobro uporabili pri primerjanju različnih vrst naložbenih priložnosti ali posojil v okviru različnih struktur.
Predpostavimo, da obstajata dve naložbeni priložnosti, vmesni depoziti v pošti in fiksne vloge na banke, na katere se je vlagatelj zožil, glede na apetit in primernost tveganja. Končni cilj vlagatelja je, da iz teh depozitov kar najbolje izkoristi in zasluži večji donos. Vendar oba instrumenta ponujata nekoliko različne obrestne mere, medtem ko Obročni depozit na pošti ponuja četrtletne poravnave za obravnavani termin.
- Znesek naložbe: Rs 10 lakh
- Obdobje naložbe: 5 let
- Bančni fiksni depozit: 7, 5% letne obresti
- Odplačni depozit na pošti: 7, 4% letne obresti, sestavljene četrtletno
Glede na ponujene letne obrestne mere se zdi, da je bančna fiksna vloga boljša možnost. Če pa vlagatelj dejansko izračuna četrtletni sestavni faktor poštnega vmesnega depozita, ima za posledico efektivno letno stopnjo / donos 7, 61%.
Zaradi te majhne spremembe s 7, 4% na 7, 61% efektivne stopnje bi investitor zaslužil skupno Rs. 4, 42, 848.28 iz tega instrumenta, medtem ko bi si zaslužil Rs. 3, 35, 469, 14 iz instrumenta bančnih vlog.
Če investitor zamudi izračun te efektivne letne stopnje, bi izgubil priložnost, da bi pridobil približno več kot Rs. 1 lakh od njegove naložbe.
Učinkovit kalkulator formule letne stopnje
Uporabite lahko naslednji kalkulator efektivne letne stopnje
| Nominalna obrestna mera | |
| Število sestavljenih obdobij | |
| Veljavna letna stopnja | |
| Efektivna letna stopnja = | ((1 + (nominalna obrestna mera / število stisnjenih obdobij)) Število zapletenih obdobij ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Priporočeni članki
To je vodnik po formuli efektivne letne stopnje. Tukaj razpravljamo o izračunu efektivne letne stopnje skupaj s praktičnimi primeri. Nudimo tudi učinkovit letni kalkulator obrestne mere s prenosljivo predlogo excel. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Kalkulator za formulo realne obrestne mere
- Formula donosa kapitala, zaposlenega | Opredelitev
- Kako izračunati efektivno obrestno mero?
- Kakšna je sedanja vrednost formule renta?