Linearna regresija v Excelu - Kako narediti linearno regresijo v Excelu?

Linearna regresija v Excelu (kazalo)

Uvod v linearno regresijo v Excelu
Metode za uporabo linearne regresije v Excelu

Uvod v linearno regresijo v Excelu

Linearna regresija je statistična tehnika / metoda, ki se uporablja za proučevanje razmerja med dvema neprekinjenima kvantitativnima spremenljivkama. V tej tehniki se za napovedovanje vrednosti odvisne spremenljivke uporabljajo neodvisne spremenljivke. Če obstaja samo ena neodvisna spremenljivka, potem gre za preprosto linearno regresijo in če je več neodvisnih spremenljivk več kot ena, potem gre za večkratno linearno regresijo. Modeli linearne regresije imajo razmerje med odvisnimi in neodvisnimi spremenljivkami, tako da v opazovane podatke prilegajo linearno enačbo. Linearno se nanaša na dejstvo, da za svoje podatke uporabljamo vrstico. Odvisne spremenljivke, ki se uporabljajo v regresijski analizi, imenujemo tudi odzivne ali predvidene spremenljivke, neodvisne spremenljivke pa imenujemo tudi pojasnjevalne spremenljivke ali prediktorji.

Linearna regresijska linija ima enačbo: Y = a + bX;

Kje:

X je pojasnjevalna spremenljivka,
Y je odvisna spremenljivka,
b je naklon premice,
a je y-prestrezanje (tj. vrednost y, ko je x = 0).

Metoda najmanjših kvadratov se običajno uporablja pri linearni regresiji, ki izračuna najboljšo črto za opazovane podatke tako, da zmanjša vsoto kvadratov odstopanja podatkovnih točk od premice.

Metode za uporabo linearne regresije v Excelu

Ta primer vas uči metode za izvajanje linearne regresijske analize v Excelu. Oglejmo si nekaj metod.

To linearno predlogo regresije Excel lahko prenesete tukaj - Linear Regression Excel predloga

1. metoda - Scatter Chart s trendno črto

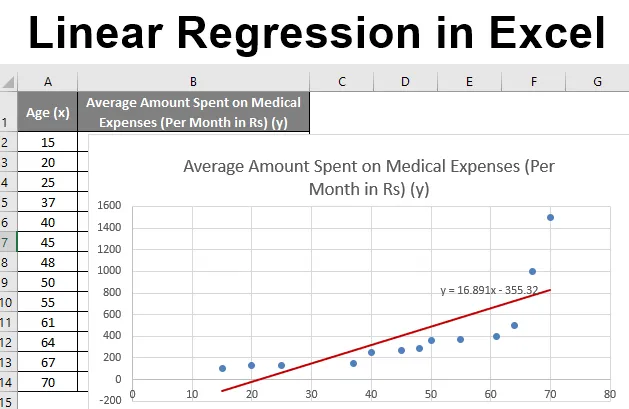
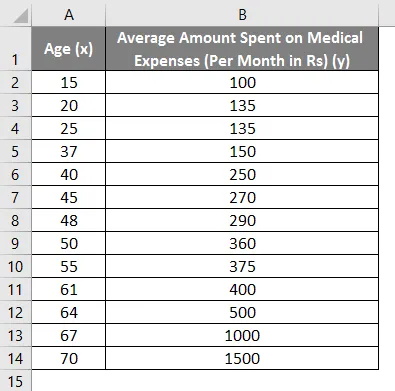
Recimo, da imamo nabor podatkov o nekaterih posameznikih z njihovo starostjo, indeksom biološke mase (BMI) in zneskom, ki so ga porabili za zdravstvene stroške v enem mesecu. Z vpogledom v posameznikove značilnosti, kot so starost in indeks telesne mase, želimo ugotoviti, kako te spremenljivke vplivajo na zdravstvene stroške, zato jih uporabimo za izvajanje regresije in oceno / napoved povprečnih zdravstvenih stroškov za nekatere posameznike. Poglejmo najprej, kako samo starost vpliva na zdravstvene stroške. Poglejmo nabor podatkov:

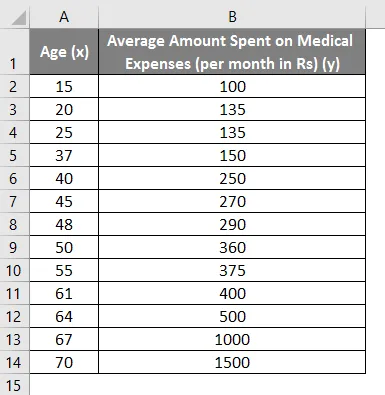
Znesek za zdravstvene stroške = b * starost + a

Izberite dva stolpca nabora podatkov (x in y), vključno z glavo.

Kliknite »Vstavi« in razširite spustni meni za »Scatter Chart« in izberite sličico »Scatter« (prva)

Zdaj se bo pojavil razplet razcepa in na tem mestu bi potegnili regresijsko črto. Če želite to narediti, z desno miškino tipko kliknite katero koli podatkovno točko in izberite »Dodaj trendno vrstico«

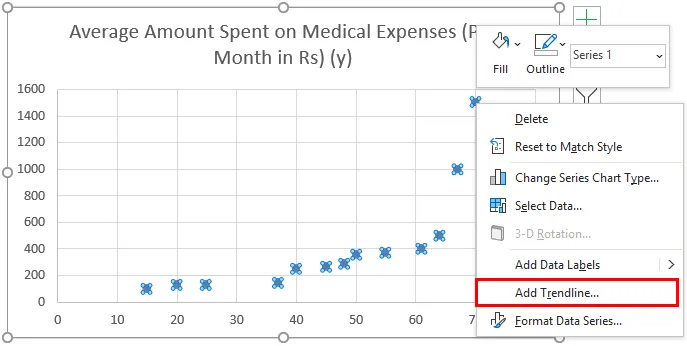
Zdaj v podoknu »Oblika trendi« na desni izberite »Linear Trendline« in »Display Equation on Chart«.

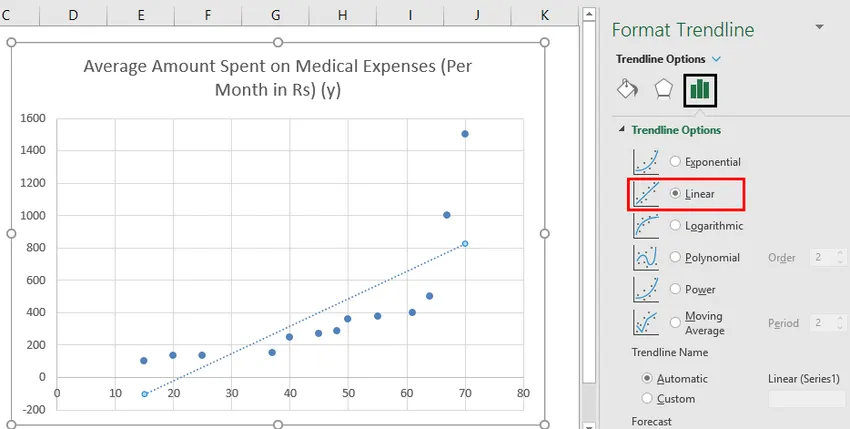
Izberite "Prikaži enačbo na grafikonu".

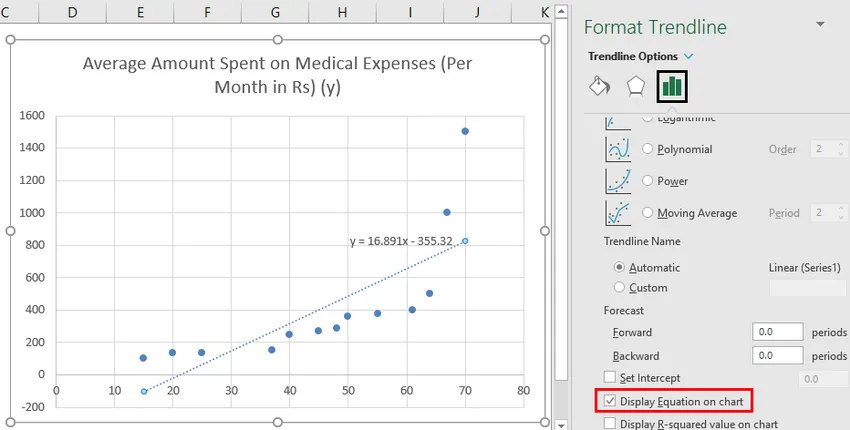
Graf lahko improviziramo v skladu z našimi zahtevami, kot je dodajanje naslovov osi, spreminjanje lestvice, barve in vrste črte.

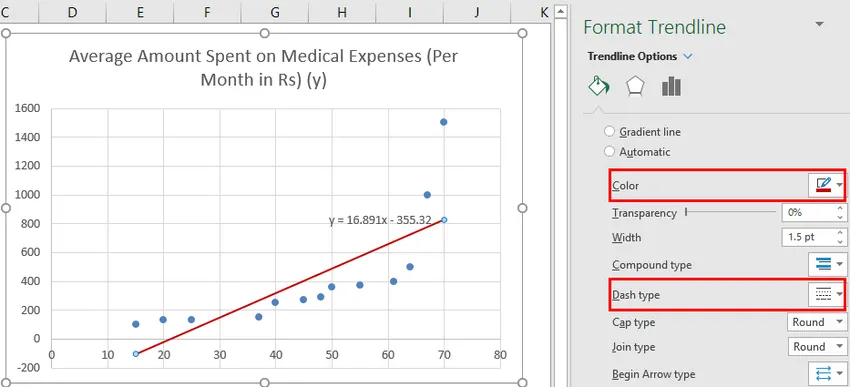
Po izboljšanju grafikona je to rezultat, ki ga dobimo.

Opomba: Pri tej vrsti regresijskega grafa mora biti odvisna spremenljivka vedno na osi y in neodvisna na osi x. Če se grafikon prikaže v obratnem vrstnem redu, bodisi preklopite osi v grafikon ali zamenjajte stolpce v naboru podatkov.

2. metoda - metoda dodatka za orodje ToolPak

Analysis ToolPak včasih ni omogočen privzeto in to moramo storiti ročno. Narediti tako:

Kliknite meni "Datoteka".

Po tem kliknite 'Možnosti'.

V polju »Upravljanje« izberite »Excel Add-Ins« in kliknite »Pojdi«

Izberite "Analysis ToolPak" -> "OK"

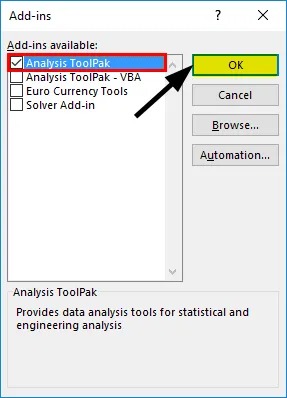
To bo dodalo orodja »Analiza podatkov« na zavihek »Podatki«. Zdaj izvajamo regresijsko analizo:

Na zavihku »Podatki« kliknite »Analiza podatkov«

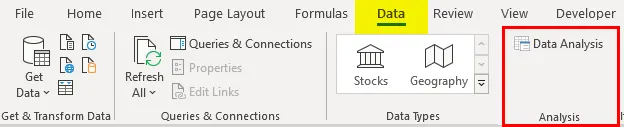
Izberite 'Regression' -> 'OK'

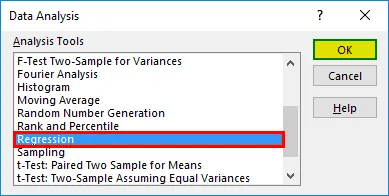
Prikaže se pogovorno okno regresije. Izberite območje vnosa Y in območje vnosa X (zdravstveni stroški in starost). V primeru večkratne linearne regresije lahko izberemo več stolpcev neodvisnih spremenljivk (na primer, če želimo videti vpliv BMI tudi na zdravstvene stroške).
Potrdite polje »Oznake«, da vključite glave.
Izberite želeno možnost 'output'.
Potrdite potrditveno polje "ostanki" in kliknite "V redu".

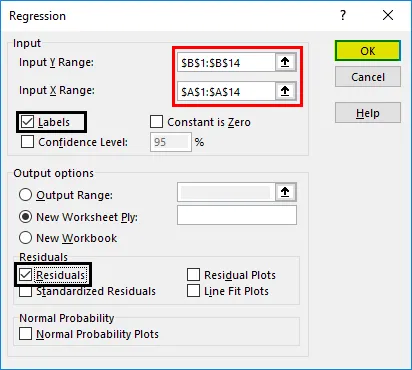
Zdaj bo naš izid za regresijsko analizo ustvarjen v novem delovnem listu z navedbo regresijske statistike, ANOVA, ostankov in koeficientov.

Razlaga izhoda:

Regresijska statistika pove, kako regresijska enačba ustreza podatkom:

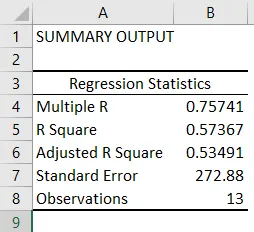
Večkratnik R je korelacijski koeficient, ki meri moč linearnega razmerja med dvema spremenljivkama. Leži med -1 in 1, njegova absolutna vrednost pa prikazuje jakost odnosa z veliko vrednostjo, ki kaže na močnejši odnos, nizka vrednost pa negativna in ničelna vrednost, ki kaže na nobeno razmerje.
Kvadrat R je koeficient odločnosti, ki se uporablja kot pokazatelj dobrega prileganja. Leži med 0 in 1, vrednost blizu 1 pa kaže na to, da se model dobro prilega. V tem primeru je 0, 57 = 57% y-vrednosti razloženo z x-vrednostmi.
Prilagojeni kvadrat R je R kvadrat, prilagojen za število prediktorjev v primeru večkratne linearne regresije.
Standardna napaka prikazuje natančnost regresijske analize.
Opazovanja prikazujejo število opazovanj modela.
Anova pove stopnjo spremenljivosti znotraj regresijskega modela.

To se običajno ne uporablja za enostavno linearno regresijo. Kljub temu „vrednosti F vrednosti“ kažejo, kako zanesljivi so naši rezultati, katerih vrednost je večja od 0, 05, kar kaže na izbiro drugega napovedovalca.

Koeficienti so najpomembnejši del, ki se uporablja za sestavljanje regresijske enačbe.

Torej, naša regresijska enačba bi bila: y = 16.891 x - 355.32. To je isto kot tisto po metodi 1 (razpršeni grafikon s trendno črto).

Zdaj, če želimo napovedati povprečne stroške zdravljenja, ko bo starost 72 let:

Torej y = 16.891 * 72 -355.32 = 860.832

Tako lahko predvidimo vrednosti y za katere koli druge vrednosti x.

Preostali podatki označujejo razliko med dejanskimi in predvidenimi vrednostmi.

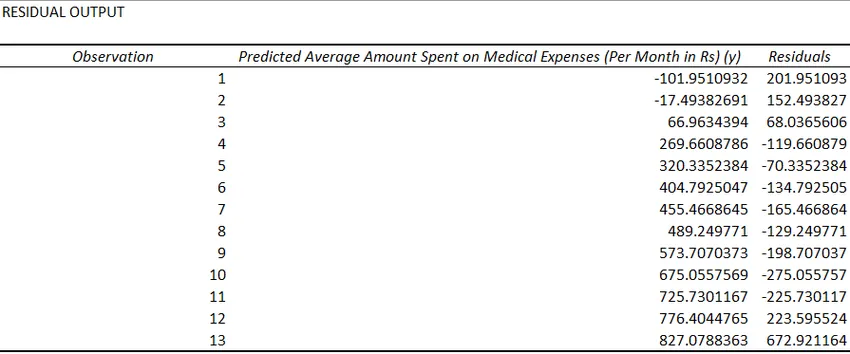
Zadnja metoda za regresijo se ne uporablja tako pogosto in zahteva statistične funkcije, kot so naklon (), prestrezanje (), korela () itd. Za izvajanje regresijske analize.

Spomniti se o linearni regresiji v Excelu

Regresijska analiza se običajno uporablja za preverjanje, ali obstaja statistično pomembna povezava med dvema sklopoma spremenljivk.
Uporablja se za napovedovanje vrednosti odvisne spremenljivke na podlagi vrednosti ene ali več neodvisnih spremenljivk.
Kadarkoli želimo linearni regresijski model prilagoditi skupini podatkov, potem je treba skrbno opazovati obseg podatkov, kot da uporabljamo regresijsko enačbo za napovedovanje katere koli vrednosti zunaj tega obsega (ekstrapolacija), potem lahko privede do napačnih rezultatov.

Priporočeni članki

To je vodnik za Linear Regression v Excelu. Tukaj razpravljamo o tem, kako narediti Linearno regresijo v Excelu skupaj s praktičnimi primeri in naloženo predlogo Excela. Ogledate si lahko tudi druge naše predlagane članke -