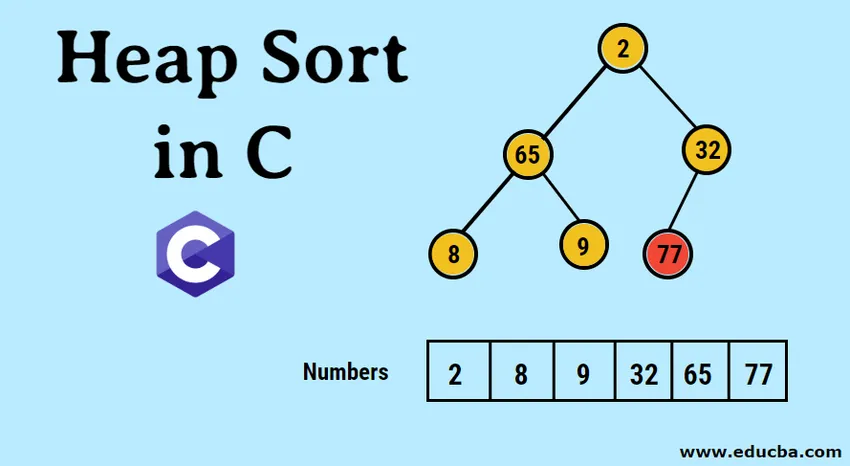
Uvod v razvrščanje gomile v C
Razvrščanje je tehnika, ki temelji na urejenosti elementov na podlagi različnih lastnosti. (Lastnosti, kot so urejanje podatkov v naraščajočem, padajočem ali abecednem vrstnem redu). En pomemben primer razvrščanja, na katerega si lahko omislimo, je naročanje izdelkov med spletnim nakupovanjem. Lahko se navezujemo na cene, priljubljenost, najnovejše in podobno. Torej obstaja veliko tehnik za to pozicioniranje elementov s sortiranjem. V tej temi bomo spoznali Heap Sort in C.
Tu bomo spoznali eno najpogostejših tehnik razvrščanja, Heap Sort, preko programskega jezika C.
Logika za Heap Sort
Kako dejansko lahko izvajamo razvrščanje v velikem obsegu? Poglejmo spodaj.
Prvič, kopica je ena izmed drevesnih podatkovnih struktur. Drevo, ki je tukaj vključeno, je vedno Popolno binarno drevo. In obstajata dve vrsti kopice
- Min - Heap: Na splošno je razporejen po naraščajočem vrstnem redu, to je, če ima nadrejeni element vozlišča vrednost, manjšo od vrednosti nadrejenih elementov vozlišča.
- Max - Heap: Na splošno so razporejeni po padajočem vrstnem redu, to je, če ima nadrejeni element vozlišča vrednost večjo od vrednosti nadrejenih elementov vozlišča.
Koraki za razvrščanje po kupu
- Ko so pridobljeni nerazvrščeni podatki s seznama, se elementi v strukturi podatkov kopice organizirajo bodisi na podlagi ustvarjanja min-heap ali max-heap.
- Prvi element z zgornjega seznama je dodan v našo paleto
- Ponovno oblikujemo tehniko strukture podatkov o glavi, enako kot prvi korak, nato pa se v našo paleto pobere največji element ali najmanjši element.
- Ponavljajoči se koraki nam pomagajo dobiti niz z razvrščenim seznamom.
Program za razvrščanje gomile v C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Najprej od uporabnika prosimo, da vnese število elementov, ki jih sprejme za razvrščanje, nato pa uporabniku dovoli vnos različnih elementov, ki jih bo razvrstil.
Sledijo koraki
- Naslednji, na katerega se bomo osredotočili, je ustvariti niz, v tem primeru max-heap matriko.
- Glavni pogoj za pridobitev matrike max - heap je preverjanje, ali nobena vrednost nadrejenega vozlišča ni manjša od njegove podrejene vrednosti vozlišča. Zamenjali se bomo, dokler ne bomo dosegli tega pogoja.
- Glavna prednost tega popolnega binarnega drevesa je, da lahko levo in desno podrejeno vozlišče nadrejenega vozlišča dostopate z vrednostmi 2 (i) + 1 in 2 * (i) + 2. Kjer sem matično vozlišče.
- Tako na ta način tukaj postavimo svoje korensko vozlišče, ki vsebuje največjo vrednost na skrajnem desnem mestu listnega vozlišča. Potem pa spet po istem postopku, tako da naslednje največje število zdaj postane korensko vozlišče.
- Sledili bomo istemu postopku, dokler v množici kup ne ostane samo eno vozlišče.
- In potem si uredimo našo množico tako, da oblikujemo popolno razvrščeno matriko v naraščajočem vrstnem redu.
- Končno tiskamo razvrščeno matriko v izhodu.
Izhod:
Izhod je priložen spodaj.
Naj vam pokažem slikovni prikaz dogajanja:
- Vneseni podatki so najprej predstavljeni v obliki enodimenzionalnega niza na naslednji način.

- Slikovni prikaz oblikovanega binarnega drevesa je naslednji:
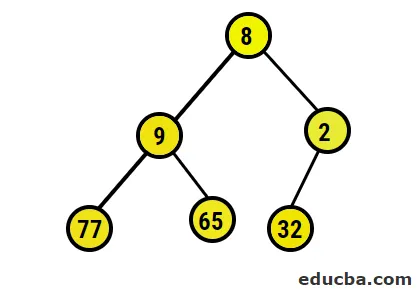
- Zdaj bomo pretvorili v max kopico tako, da bomo zagotovili, da so vsa nadrejena vozlišča vedno večja od podrejenih vozlišč. Kot je omenjeno v izhodu pod nizom razvrščenega niza, bi bil slikovni prikaz:
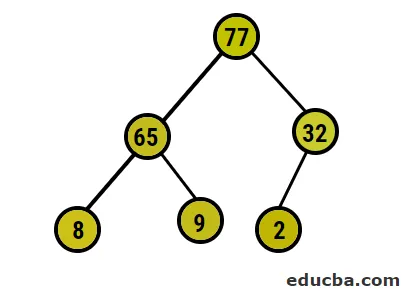
- Po tem bomo koreninsko vozlišče zamenjali s skrajnim listnim vozliščem in ga nato izbrisali z drevesa. Listje vozlišče bi bil koren zdaj in spet isti postopek e sledil, da bi spet dobili najvišji element v korenu
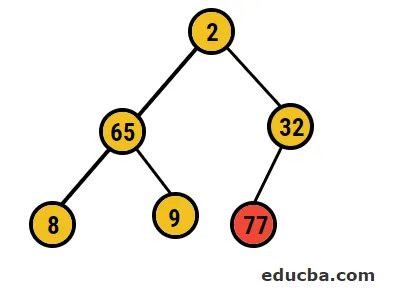
- Torej v tem primeru iz tega drevesa izbrišemo 77 števk in jih damo v naš razvrščeni niz in postopek se ponovi.
Zgoraj smo ga videli za oblikovanje max kopice. Isti postopek se obravnava tudi pri nastajanju nizov min. Kot je razloženo zgoraj, je edina razlika v razmerju med elementi nadrejenega in nadrejenega vozlišča.
Lahko poskusite oblikovati vrsto kup v padajočem vrstnem redu?
Zaključek
Čeprav obstaja veliko tehnik sortiranja, sorta gomila velja za eno boljših tehnik sortiranja zaradi svoje časovne in prostorske zapletenosti. Časovna zapletenost vseh najboljših, povprečnih in najslabših primerov je O (nlogn), kjer je najslabša kompleksnost boljša od najslabše zapletenosti Quicksort, prostorska kompleksnost pa O (1).
Priporočeni članki
To je priročnik za razvrščanje gomile v C. Tukaj razpravljamo o logiki in korakih za razvrščanje kopice s kodo vzorca in izhodom skupaj s slikovnimi predstavitvami. Za več informacij si lahko ogledate tudi naslednje članke -
- Razvrsti po Javi
- Izbira Razvrsti v Javi
- Palindrome v programu C
- Vzorci v C programiranju
- Razvrščanje po skupinah C ++ (algoritem)
- Razvrstite v Python
- C Programiranje množenja matrike