Kaj je GLM v R?
Generalizirani linearni modeli so podmnožica linearnih regresijskih modelov in učinkovito podpirajo normalne distribucije. Za podporo temu priporočamo uporabo funkcije glm (). GLM dobro deluje s spremenljivko, kadar odstopanje ni konstantno in se distribuira normalno. Določena je funkcija povezave, ki transformira odzivno spremenljivko tako, da ustreza ustreznemu modelu. LM model je narejen tako z družino kot s formulo. Model GLM ima tri ključne komponente, imenovane naključna (verjetnost), sistematična (linearni napovedovalec), komponenta povezave (za funkcijo logit). Prednost uporabe glm je, da imajo fleksibilnost modela, ne potrebujejo konstantnega odstopanja in ta model ustreza najvišji oceni verjetnosti in njegovim razmerjem. V tej temi bomo spoznali GLM v R.
GLM funkcija
Sintaksa: glm (formula, družina, podatki, uteži, podmnožica, Start = null, model = TRUE, metoda = ””…)
Tu spadajo družinski tipi (vključujejo modele modelov): binom, Poisson, Gaussian, gama, kvazi. Vsaka distribucija ima drugačno uporabo in jo je mogoče uporabiti tako v razvrščanju kot v napovedi. Ko je model gaussov, bi moral biti odziv resnično celo število.
In kadar je model binomen, bi morali biti odziv razredi z binarnimi vrednostmi.
In ko je model Poisson, bi moral biti odziv ne-negativen z numerično vrednostjo.
In kadar je model gama, bi moral biti odziv pozitivna številčna vrednost.
glm.fit () - Prilagoditev modelu
Lrfit () - označuje logistično regresijo.
update () - pomaga pri posodabljanju modela.
anova () - izbirni test.
Kako ustvariti GLM v R?
Tukaj bomo videli, kako ustvariti enostaven generaliziran linearni model z binarnimi podatki z uporabo funkcije glm (). In z nadaljevanjem nabora podatkov o drevesih.
Primeri
// Uvoz knjižnicelibrary(dplyr)
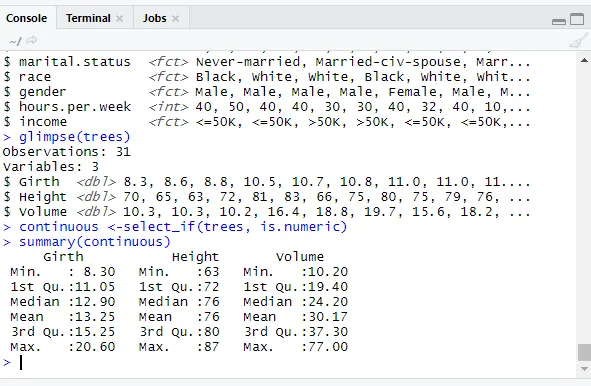
glimpse(trees)

Za ogled kategoričnih vrednosti so dodeljeni faktorji.
levels(factor(trees$Girth))
// Preverjanje neprekinjenih spremenljivk
library(dplyr)
continuous <-select_if(trees, is.numeric)
summary(continuous)
// Vključitev nabora dreves v R search Pathattach (drevesa)
x<-glm(Volume~Height+Girth)
x
Izhod:
| Klic: glm (formula = glasnost ~ višina + obseg)
Koeficienti: (Prestrezanje) Višina pasu -57.9877 0.3393 4.7082 Stopnje svobode: 30 Skupaj (tj. Nično); 28 Preostali Ničelno odstopanje: 8106 Preostalo odstopanje: 421, 9 AIC: 176, 9 |
summary(x)
| Pokliči:
glm (formula = prostornina ~ višina + obseg) Preostali delivanci: Min 1Q Mediana 3Q Max -6.4065 -2.6493 -0.2876 2.2003 8.4847 Koeficienti: Oceni št. Napaka t vrednost Pr (> | t |) (Prestrezanje) -57.9877 8.6382 -6.713 2.75e-07 *** Višina 0, 3393 0, 1302 2, 607 0, 0145 * Obseg 4, 7082 0, 2643 17, 816 <2e-16 *** - Signif. kode: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1 (Disperzijski parameter za družino Gauss je bil 15.06862) Ničelno odstopanje: 8106, 08 na 30 stopinj svobode Preostalo odstopanje: 421, 92 na 28 stopinjah svobode AIC: 176, 91 Število ponovitev Fisherjevega točkovanja: 2 |
Izhod funkcije povzetka poda klice, koeficiente in preostale vrednosti. Zgornji odziv kaže, da sta koeficient višine in pasu nepomembna, saj je verjetnost zanje manjša od 0, 5. Obstajata dve različici odklona, imenovana ničelna in preostala. Končno je ocenjevanje ribičev algoritem, ki rešuje največ verjetnosti. Pri binomu je odziv vektor ali matrica. cbind () se uporablja za vezanje vektorjev stolpcev v matriki. Za pridobitev podrobnih informacij o primernem povzetku se uporabljajo.
Če želite narediti kot preizkus napa, se izvede naslednja koda.
step(x, test="LRT")
Start: AIC=176.91
Volume ~ Height + Girth
Df Deviance AIC scaled dev. Pr(>Chi)
421.9 176.91
- Height 1 524.3 181.65 6.735 0.009455 **
- Girth 1 5204.9 252.80 77.889 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Call: glm(formula = Volume ~ Height + Girth)
Coefficients:
(Intercept) Height Girth
-57.9877 0.3393 4.7082
Degrees of Freedom: 30 Total (ie Null); 28 Residual
Null Deviance: 8106
Residual Deviance: 421.9 AIC: 176.9
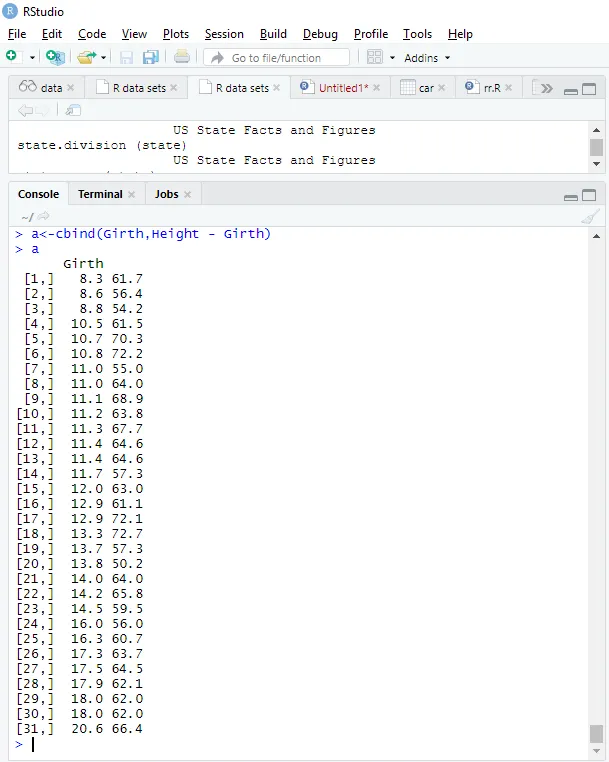
Model ustreza
a<-cbind(Height, Girth - Height)
> a
povzetek (drevesa)
Girth Height Volume
Min. : 8.30 Min. :63 Min. :10.20
1st Qu.:11.05 1st Qu.:72 1st Qu.:19.40
Median :12.90 Median :76 Median :24.20
Mean :13.25 Mean :76 Mean :30.17
3rd Qu.:15.25 3rd Qu.:80 3rd Qu.:37.30
Max. :20.60 Max. :87 Max. :77.00
Da dobimo ustrezen standardni odklon
apply(trees, sd)
Girth Height Volume
3.138139 6.371813 16.437846
predict <- predict(logit, data_test, type = 'response')
Nato se sklicujemo na spremenljivko odzivnosti štetja, da bi oblikovali dober odziv. Za izračun tega bomo uporabili nabor podatkov USAccDeath.
V konzolo R vnesite naslednje delčke in si oglejte, kako se na njih izvajata štetje let in kvadrat.
data("USAccDeaths")
force(USAccDeaths)
// Analizirati leto od 1973-1978.
disc <- data.frame(count=as.numeric(USAccDeaths), year=seq(0, (length(USAccDeaths)-1), 1)))
yearSqr=disc$year^2
a1 <- glm(count~year+yearSqr, family="poisson", data=disc)
summary(a1)
| Pokliči:
glm (formula = štetje ~ leto + letoSqr, družina = "poisson", podatki = disk) Preostali delivanci: Min 1Q Mediana 3Q Max -22.4344 -6.4401 -0.0981 6.0508 21.4578 Koeficienti: Oceni št. Napaka z vrednost Pr (> | z |) (Prestrezanje) 9.187e + 00 3.557e-03 2582.49 <2e-16 *** leto -7.207e-03 2.354e-04 -30.62 <2e-16 *** letoSqr 8.841e-05 3.221e-06 27.45 <2e-16 *** - Signif. kode: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1 (Parameter disperzije za družino Poisson, ki velja za 1) Ničelno odstopanje: 7357, 4 na 71 stopinjah svobode Preostalo odstopanje: 6358, 0 na 69 stopinjah svobode AIC: 7149.8 Število ponovitev Fisherjevega točkovanja: 4 |
Za preverjanje ustreznosti modela lahko uporabite naslednji ukaz
ostanke preskusa. Iz spodnjega rezultata je vrednost 0.
1 - pchisq(deviance(a1), df.residual(a1))
Uporaba QuasiPoisson družine za večjo razliko v danih podatkih
a2 <- glm(count~year+yearSqr, family="quasipoisson", data=disc)
summary(a2)
| Pokliči:
glm (formula = štetje ~ leto + letoSqr, družina = "kvazipoisson", podatki = disk) Preostali delivanci: Min 1Q Mediana 3Q Max -22.4344 -6.4401 -0.0981 6.0508 21.4578 Koeficienti: Oceni št. Napaka t vrednost Pr (> | t |) (Prestrezanje) 9.187e + 00 3.417e-02 268.822 <2e-16 *** letnik -7.207e-03 2.261e-03 -3.188 0, 00216 ** letoSqr 8.841e-05 3.095e-05 2.857 0.00565 ** - (Disperzijski parameter za družino kvazipoissonov je bil 92, 28857) Ničelno odstopanje: 7357, 4 na 71 stopinjah svobode Preostalo odstopanje: 6358, 0 na 69 stopinjah svobode AIC: NA Število ponovitev Fisherjevega točkovanja: 4 |
Primerjava Poissonove z binomno vrednostjo AIC se bistveno razlikuje. Lahko jih analiziramo z natančnostjo in razmerjem priklica. Naslednji korak je preverjanje, da je odstopanje ostankov sorazmerno s srednjo vrednostjo. Nato lahko načrtujemo uporabo knjižnice ROCR za izboljšanje modela.
Zaključek
Zato smo se osredotočili na poseben model, imenovan generalizirani linearni model, ki pomaga pri fokusiranju in oceni parametrov modela. To je predvsem možnost stalne spremenljivke odziva. In videli smo, kako glm ustreza R vgrajenim paketom. So najbolj priljubljeni pristopi za merjenje podatkov štetja in zanesljivo orodje za klasifikacijske tehnike, ki jih uporablja podatkovni znanstvenik. R jezik seveda pomaga pri opravljanju zapletenih matematičnih funkcij
Priporočeni članki
To je vodnik za GLM v R. Tukaj razpravljamo o funkciji GLM in kako ustvariti GLM v R s primeri drevesnih podatkovnih nizov in izhodom. Če želite izvedeti več, si oglejte tudi naslednji članek -
- R Programski jezik
- Velika podatkovna arhitektura
- Logistična regresija v R
- Posel z velikimi podatki o analitiki
- Poisson regresija v R | Izvajanje Poissonove regresije