
Uvod v standardne primere odklona
Obstaja dovolj primerov standardnih odstopanj. Standardni odklon je merilo razpršenosti nabora podatkov, tj. Kako so razporejene številke. Koristno je za primerjavo različnih nizov podatkov, ki imajo lahko enako srednjo vrednost, vendar različen obseg. Naslednji različni primer standardnega odklona daje razumevanje najpogostejših vrst situacij, kjer se izračuna standardno odstopanje in kako je mogoče izračunati isto
Primeri standardnega odklona
Spodaj so primeri Standardnega odstopanja
Standardno odstopanje - primer št. 1
Zaloga družbe Z prodaja za 50 dolarjev na delnico in enake ponudbe po izplačilih za naslednje leto:
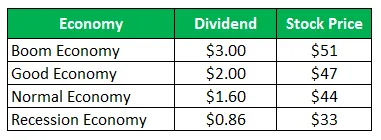
Izračunajte standardni odklon, če so podani vsi štirje scenariji enako verjetno.
Rešitev:
Izračuni donosa zadrževanja (HPR) so naslednji:
Formula HPR
HPR = ((vrednost konca obdobja - prvotna vrednost) + dohodek) / prvotna vrednost) * 100
Za ekonomijo razcveta
- HPR (razcvet) = ((51-50) + 3) / 50 = 8, 00%
- HPR (dobro) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normalno) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recesija) = ((33-50) + 0, 86) / 50 = -32, 28%
Izračun pričakovanega donosa
Ker so vsi scenariji enako verjetni, bo verjetno tudi verjetnost vseh
Formula pričakovane donosnosti
Pričakovani donos = (verjetnost razcveta * vrnitev iz razcveta) + (verjetnost dobrega * vrnitev od dobrega) + (verjetnost normalnega * vrnitev od normalnega) + (verjetnost recesije * vrnitev iz recesije)
- Pričakovani donos = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Pričakovana donosnost = -8, 77%
Izračun standardnega odstopanja
Formula variacije
Odstopanje = (Verjetnost razcveta * (Vrnitev iz strele - Skupni pričakovani donos) 2) + (Verjetnost dobrega * (Vrnitev iz dobrega - Skupni pričakovani donos) 2) + (Verjetnost normalnega * (Vrnitev iz običajnega - Skupni pričakovani donos) 2 ) + (verjetnost recesije * (vrnitev iz recesije - skupni pričakovani donos) 2)
- Odstopanje = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Variance = 219, 95
Formula standardnega odklona
Standardno odstopanje bo Square Root of Variance
Standardno odstopanje = √ varianta
- Standardno odstopanje = √ 219, 95
- Standardno odstopanje = 14, 83%
Primer standardnega odklona - 2
Standardno odstopanje v primeru dveh družb v portfelju
Skupna zaloga družbe A prodaja za 28 dolarjev na delnico in enake ponudbe po izplačilih za naslednje leto

Navadna zaloga družbe B se prodaja za 93 dolarjev na delnico in enake ponudbe po izplačilih za naslednje leto:

(a) Izračunajte standardni odklon podjetja A
(b) Izračunajte standardni odklon podjetja B
(c) Izračunajte standardni odklon portfelja, če je polovica naložbe izvedena v družbi A, polovica pa v družbi B
Rešitev:
Za podjetje A
Izračuni donosa dobe zadrževanja (HPR)
Formula HPR
HPR = ((vrednost konca obdobja - prvotna vrednost) + dohodek) / prvotna vrednost) * 100
- HPR (razcvet) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normalno) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recesija) = ((38-28) + 5) / 28 = 53, 57%
Izračun pričakovanega donosa podjetja A
Formula pričakovane donosnosti
Pričakovani donos = (verjetnost razcveta * vrnitev iz strele) + (verjetnost normalnega * vrnitev iz običajnega) + (verjetnost recesije * vrnitev iz recesije)
- Pričakovani donos = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Pričakovani donos = 3, 84%
Izračun družbe Standard Deviation A
Formula variacije
Odstopanje = (Verjetnost razcveta * (Vrnitev iz strele - Skupni pričakovani donos) 2) + (Verjetnost normalnega * (Vrnitev iz običajnega - Skupni pričakovani donos) 2 ) + (Verjetnost recesije * (Vrnitev iz recesije - Skupni pričakovani donos) 2)
- Odstopanje = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Variacija = 895, 15
Formula standardnega odklona
Standardno odstopanje bo Square Root of Variance
Standardno odstopanje = √ varianta
- Standardno odstopanje = √ 895, 15
- Standardno odstopanje = 29, 92%
Za podjetje B
Izračuni donosa dobe zadrževanja (HPR)
Formula HPR
HPR = ((vrednost konca obdobja - prvotna vrednost) + dohodek) / prvotna vrednost) * 100
HPR (razcvet) = ((200–93) +7) / 93 = 122, 58%
HPR (normalno) = ((105–93) + 5, 50 / 93 = 18, 82%
HPR (recesija) = ((4-93) +2) / 93 = -93, 55%
Izračun pričakovanega donosa
Formula pričakovane donosnosti
Pričakovani donos = (verjetnost razcveta * vrnitev iz strele) + (verjetnost normalnega * vrnitev iz običajnega) + (verjetnost recesije * vrnitev iz recesije)
- Pričakovani donos = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Pričakovani donos = 43, 04%
Izračun standardnega odstopanja
Formula variacije
Odstopanje = (Verjetnost razcveta * (Vrnitev iz strele - Skupni pričakovani donos) 2) + (Verjetnost normalnega * (Vrnitev iz običajnega - Skupni pričakovani donos) 2 ) + (Verjetnost recesije * (Vrnitev iz recesije - Skupni pričakovani donos) 2)
- Odstopanje = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (–93, 55– (43, 04)) 2
- Variacija = 6783, 65
Formula standardnega odklona
Standardno odstopanje bo Square Root of Variance
Standardno odstopanje = √ varianta
- Standardno odstopanje = 836783, 65
- Standardno odstopanje = 82, 36%
Izračun pričakovane donosnosti in standardnega odstopanja polovice portfelja, vložene v družbo A in polovico v družbo B.
Standardno odstopanje podjetja A = 29, 92%
Standardno odstopanje podjetja B = 82, 36%
Teža podjetja A = 0, 50
Teža podjetja B = 0, 50
Formula standardnega odstopanja portfelja
Standardno odstopanje portfelja = (Teža podjetja A * Pričakovani donos podjetja A) + ((Teža podjetja B * Pričakovani donos podjetja B)
- Standardno odstopanje portfelja = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardno odstopanje portfelja = 56, 14%
Analiza
Standardno odstopanje portfelja je nižje kot pri posameznih delnicah, ker so zaloge v različnih zalogah raznovrstne. Diverzifikacija vodi k zmanjšanju tveganja, razen če obstaja dober korelacija med donosnostjo portfeljskih naložb.
Sklep - Standardni primeri odklona
Standardni odklon meri razpršenost nabora podatkov, ki je sorazmerna z njegovo srednjo vrednostjo. Izračuna se kot kvadratni koren variance. Večji kot je standardni odklon varščine, večja bo odstopanje med ceno in srednjo vrednostjo, kar kaže, da je cenovni razpon velik. Zgoraj navedeni primeri so nekateri primeri standardnega odklona na različne načine. Obstajajo tudi različni drugi primeri, ki kažejo, da se standardni odmik lahko izračuna z uporabo drugih podatkov.
Priporočeni članki
To je vodnik za standardne primere odstopanja. Tukaj obravnavamo različne primere standardnega odklona skupaj s podrobno razlago . Za več informacij si lahko ogledate tudi naslednje članke -
- Primer fiksnih stroškov
- Primer spremenljivih stroškov
- Primer kvantitativnih raziskav
- Primeri monopolne konkurence