
Vzorčna standardna odstopna formula (kazalo)
- Formula
- Primeri
Vzorčna standardna odstopna formula
V statistiki je standardni odklon v bistvu merilo za iskanje razpršenosti nabora podatkov od srednje vrednosti nabora podatkov. Izmeri razdaljo te podatkovne točke in srednjo vrednost. Tako višji je standardni odmik, večja bo razpršenost in podatkovne točke bodo daleč od povprečja. Podobno manjši standardni odklon pomeni, da bodo podatkovne točke bližje srednji vrednosti. Zelo koristno je pri primerjanju nizov podatkov, ki imajo lahko isto srednjo vrednost, vendar drugačen razpon.
Običajno izračunajte standardni odklon podatkov o prebivalstvu, včasih pa so podatki o prebivalstvu tako ogromni, da za to ni mogoče najti standardnega odstopanja. V tem primeru se izračuna standardni standardni odklon vzorca, ki bo postal reprezentativni standardni odklon. Tako bomo domnevali, da je vzorec pravilna reprezentacija populacije in se bomo v tem članku osredotočili na vzorčni standardni odklon.
Recimo, da imate podatkovni niz X s podatkovnimi točkami (X1, X2 …… ..Xn).
Formulo za standardni odklon populacije poda:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Če vam ni dana celotna populacija in imate samo vzorec (recimo X je vzorčni nabor podatkov populacije), potem formula za standardni odklon vzorca poda:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Kje:
- X i - i th vrednost nabora podatkov
- X m - srednja vrednost nabora podatkov
- n - Skupno število podatkovnih točk
Formula lahko na začetku izgleda zmedeno, vendar je treba resnično delati. Sledijo koraki za izračun standardnega odklona vzorca:
- Poiščite število točk v nizu podatkov, tj n
- Nato je naslednji korak iskanje srednje vrednosti vzorca. V bistvu je povprečje vseh vrednosti.
- Po tem za vsako podatkovno točko poiščite razliko le-te od srednje in jo nato kvadratite.
- Vzemite vse vrednosti v zgornjem koraku in jih delite z n-1.
- Zadnji korak je, da vzamemo kvadratni koren zgoraj izračunanega števila.
Obstaja še en način izračunavanja populacije in standardnega odklona s pomočjo funkcije STDEV.P () za standardni odklon populacije in funkcije STDEV.S () za standardni odklon vzorca v excelu.
Primeri vzorčne standardne odstopne formule (s predlogo Excel)
Vzemimo primer, da bolje razumemo izračun vzorčnega standardnega odstopanja.
To vzorčno predlogo za standardno odstopanje Formule Excel lahko prenesete tukaj - Vzorčna predloga za standardno odstopanje Formula ExcelVzorčna standardna odstopna formula - Primer 1
Recimo, da imamo dva vzorčna podatkovna niza A&B in vsak vsebuje 20 naključnih podatkovnih točk in ima enako srednjo vrednost. Izračunajte vzorčno standardno odstopanje za niz podatkov A&B.
Rešitev:
Srednja vrednost se izračuna kot:
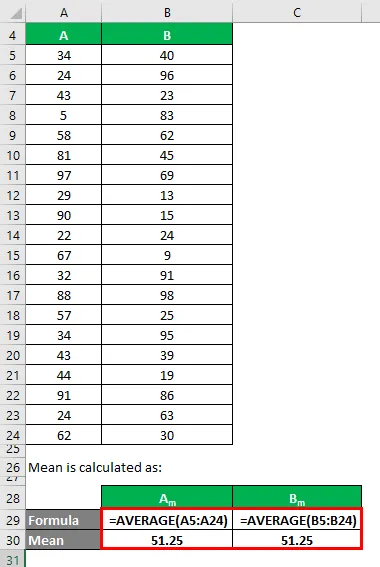
- Srednja vrednost nabora podatkov A = 51, 25
- Srednja vrednost nabora podatkov B = 51, 25
Zdaj moramo izračunati razliko med podatkovnimi točkami in srednjo vrednostjo.
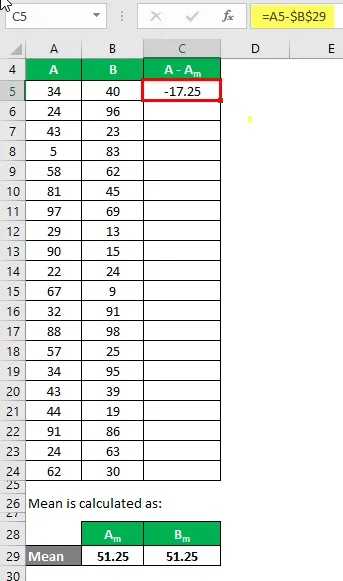
Podobno izračunajte za vse naloge podatkov A.
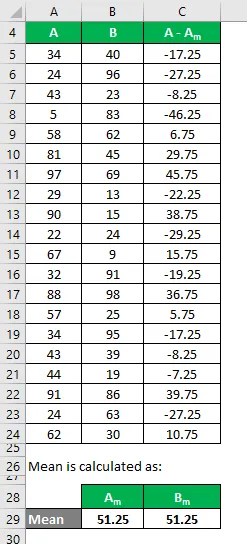
Podobno izračunajte tudi za niz B.
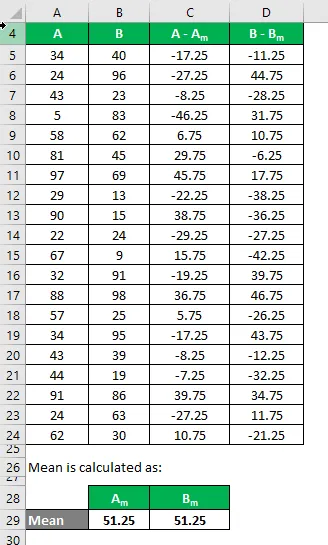
Izračunajte kvadrat razlike za oba niza podatkov A in B.
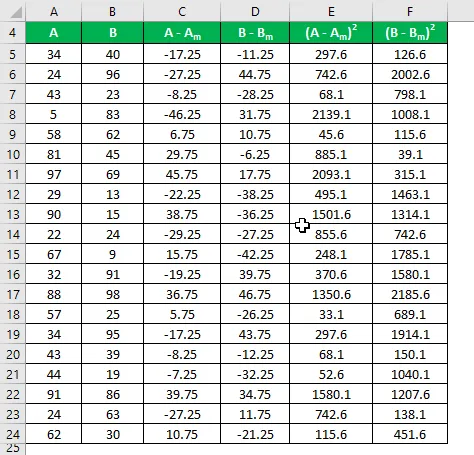
Vzorec Standardno odstopanje se izračuna po spodnji formuli
Vzorec standardno odstopanje = √ (Σ (X i - X m ) 2 / (n - 1))
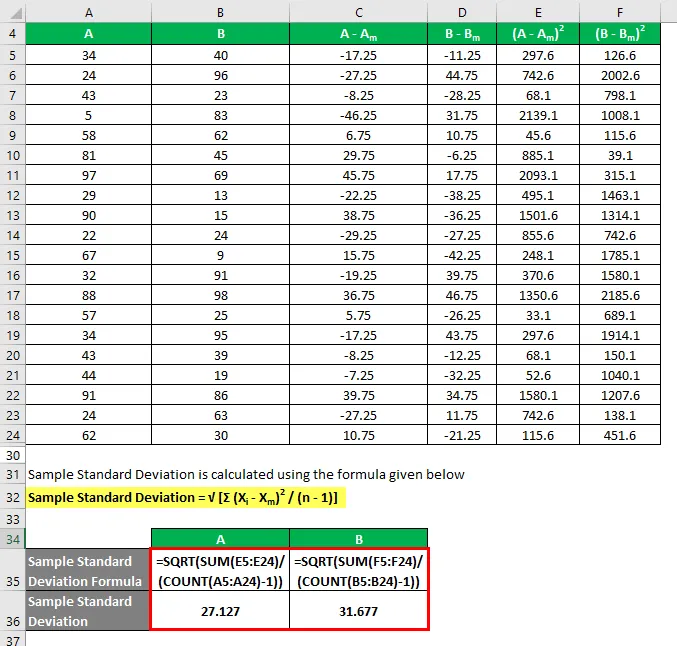
Če vidite tukaj, čeprav imata oba nabora podatkov isto srednjo vrednost, ima B bolj standardni odklon kot A, kar pomeni, da so podatkovne točke B bolj razpršene od A.
Vzorčna standardna odstopna formula - primer # 2
Recimo, da ste zelo naklonjen vlagatelju in želite vložiti denar na delnico. Ker je vaš apetit za tveganje nizek, želite vlagati v varne zaloge, ki imajo nižji standardni odklon. Vaš finančni svetovalec vam je predlagal 4 zaloge, med katerimi lahko izbirate. Med temi štirimi zalogami želite izbrati 2 zalogi in to se boste odločili na podlagi nižjega standardnega odstopanja.
Informacije o njihovih zgodovinskih poročilih ste dobili v zadnjih 15 letih.
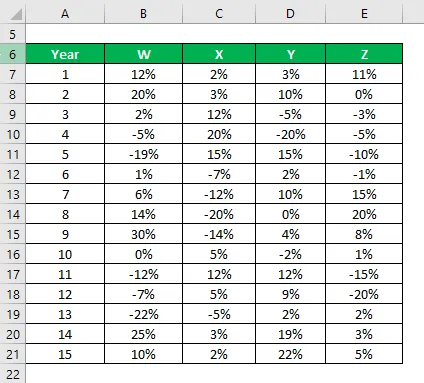
Rešitev:
Vzorec Standardno odstopanje se izračuna po formuli excel
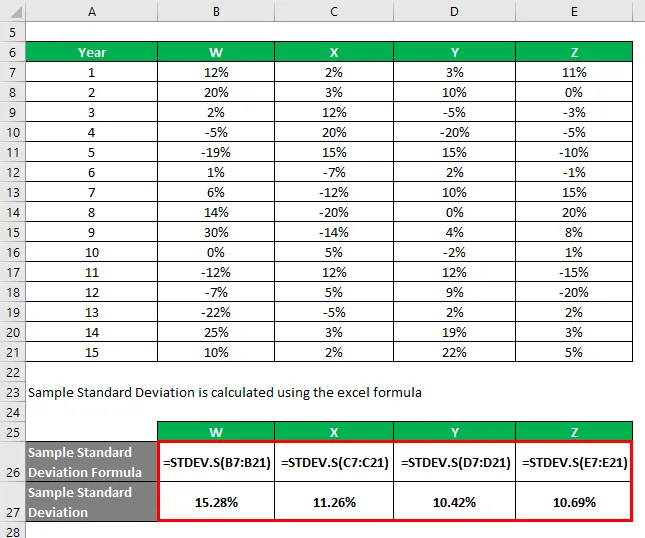
Na podlagi informacij in vzorčnega standardnega odklona boste izbrali zaloge Y in Z, ki jih želite vložiti, saj imajo najnižjo standardno odstopanje.
Pojasnilo
Razpravljamo o pomenu standardnega odstopanja od statističnega stališča, vendar ima tudi ključno vlogo, če govorimo o finančnem stališču. Pri financah je v bistvu merilo tveganja, ki ga naložba nosi, in kako tvegana je. Na podlagi tveganja, ki ga ima naložba, lahko vlagatelji izračunajo najmanjši donos, ki ga potrebujejo za nadomestilo tega tveganja. Tako kot v zgornjem primeru, ker imata Y in Z manjši standardni odklon, pomeni, da je pri vračanju teh staležev manj variabilnosti, zato so manj tvegane. Pri uporabi orodja s standardnim odklonom moramo upoštevati, da so skrajne vrednosti ali odbitki zelo prizadeti. Ti odpuščaji lahko izkrivijo vrednost standardne deviacije.
Ustreznost in uporabe vzorčne standardne odstopne formule
Standardni odklon pomaga vlagateljem in analitikom, da najdejo razmerje med tveganjem in nagrado ali ostrino za naložbo. V bistvu lahko vsakdo zasluži netvegano stopnjo donosa z vlaganjem v zakladnice in varčne vrednostne papirje. Toda donosnost nad tem je presežek donosa in za dosego tega je stopnja ostrega razmerja tista stopnja tveganja, ki jo je treba prevzeti:
Ostro razmerje = (donosnost naložbe - brez tveganja) / standardno odstopanje
Tako da je višje razmerje Sharpe, boljša je naložba.
Kot smo rekli, je standardno odstopanje merilo tveganja, vendar nižja vrednost standardnega odklona ni vedno prednostna. Če ima vlagatelj večji apetit za tveganje in želi investirati bolj agresivno, bo pripravljen tvegati in raje razmeroma višji standardni odklon kot vlagatelj, ki je naklonjen tveganju. Torej je vse odvisno od stopnje tveganja, ki jo je vlagatelj pripravljen prevzeti.
Priporočeni članki
To je vodnik za vzorčno standardno odstopanje formule. Tukaj razpravljamo o tem, kako izračunati vzorčno standardno odstopanje skupaj s praktičnimi primeri in naložljivo predlogo Excela. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Primeri formule variacije prebivalstva
- Kalkulator za relativno standardno odstopanje
- Kako izračunati standardno normalno porazdelitev?
- Izračun binomne porazdelitve