
Formula za napako (kazalo)
- Območja napake
- Primeri formule marže napake (s predlogo Excel)
- Razlika napake Kalkulator formule
Območja napake
V statistiki izračunamo interval zaupanja, da vidimo, kje bo vrednost podatkov vzorčne statistike padla. Razpon vrednosti, ki so pod statistiko vzorca v intervalu zaupanja, je znan kot marža napake. Z drugimi besedami, v bistvu gre za stopnjo napake v vzorčni statistiki. Višja stopnja napake bo manjša zaupanje v rezultate, ker je stopnja odstopanja pri teh rezultatih zelo visoka. Kot pove že njegovo ime, je meja napake razpon vrednosti nad in pod dejanskimi rezultati. Če na primer dobimo odgovor v anketi, v kateri je 70% ljudi odgovorilo "dobro", napak pa 5%, to pomeni, da na splošno 65% do 75% prebivalstva misli, da je odgovor "dober" .
Formula za napako -
Margin of Error = Z * S / √n
Kje:
- Z - Z ocena
- S - Standardno odstopanje prebivalstva
- n - Velikost vzorca
Druga formula za izračun stopnje napake je:
Margin of Error = Z * √((p * (1 – p)) / n)
Kje:
- p - vzorčni delež (del uspešnega vzorca)
Zdaj, če želite poiskati želeno oceno z, morate poznati interval zaupanja vzorca, ker je ocena Z odvisna od tega. Spodaj je tabela, da si ogledate razmerje intervala zaupanja in ocene z:
| Interval zaupanja | Z - ocena |
| 80% | 1.28 |
| 85% | 1, 44 |
| 90% | 1.65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Ko poznate interval zaupanja, lahko uporabite ustrezno vrednost z in od tam izračunate mejo napake.
Primeri formule marže napake (s predlogo Excel)
Vzemimo primer, da bolje razumemo izračun marže napake.
To predlogo o predlogu napake lahko prenesete tukaj - Oblika predloge napakFormula napake - Primer # 1
Recimo, da izvajamo anketo, da vidimo, kakšna je ocena, ki jo dobijo študentje na univerzi. Naključno smo izbrali 500 učencev in vprašali njihovo oceno. Povprečje tega je 2, 4 od 4, standardni odklon pa je 30%. Predpostavimo, da je interval zaupanja 99%. Izračunajte mejo napake.
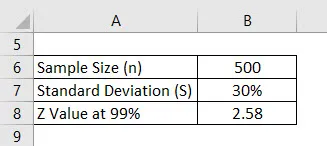
Rešitev:
Število napak se izračuna po spodnji formuli
Območje napake = Z * S / √n
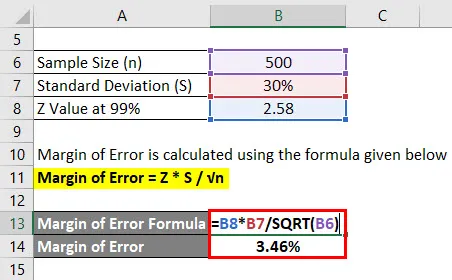
- Število napake = 2, 58 * 30% / √ (500)
- Napaka = 3, 46%
To pomeni, da je z 99-odstotnim zaupanjem povprečna ocena študentov 2, 4 plus ali minus 3, 46%.
Formula napake - Primer # 2
Recimo, da na trg lansirate nov zdravstveni izdelek, vendar ste zmedeni, kateri okus bo ljudem všeč. Zmedeni ste med okusom po banani in okusom vanilje ter ste se odločili za anketo. Vaše prebivalstvo je 500.000, kar je vaš ciljni trg, in od tega ste se odločili vprašati mnenje 1000 ljudi in to bo vzorec. Predpostavimo, da je interval zaupanja 90%. Izračunajte mejo napake.
Rešitev:
Ko je raziskava končana, ste vedeli, da je 470 ljudem všeč okus banane, 530 pa jih je zaprosilo za aromo vanilije.
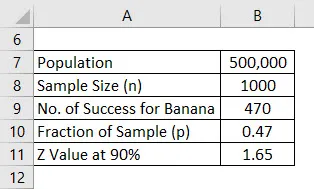
Število napak se izračuna po spodnji formuli
Območje napake = Z * √ ((p * (1 - p)) / n)
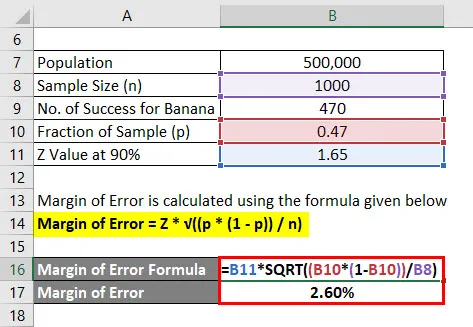
- Število napake = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Napaka = 2, 60%
Torej lahko rečemo, da je z 90-odstotno samozavestjo 47% vseh ljudi všeč okusu banane plus ali minus 2, 60%.
Pojasnilo
Kot je razloženo zgoraj, nam napaka pomaga razumeti, ali je velikost vzorca vaše ankete ustrezna ali ne. V primeru, da je napaka pri marži prevelika, je mogoče, da je naša velikost vzorca premajhna in jo moramo povečati, da se rezultati vzorcev bolj ujemajo z rezultati populacije.
Obstaja nekaj scenarijev, pri katerih meja napake ne bo koristila in nam ne bo pomagala pri sledenju napake:
- Če vprašanja iz ankete niso zasnovana in ne pomagajo pri iskanju potrebnega odgovora
- Če imajo ljudje, ki se odzivajo na anketo, nekaj pristranskosti glede izdelka, za katerega se anketa izvaja, potem tudi rezultat ne bo zelo natančen
- Če je vzorec, ki ga je sam izbral, pravi predstavnik populacije, bodo tudi v tem primeru rezultati izpuščeni.
Poleg tega je ena velika domneva, da je prebivalstvo normalno porazdeljeno. Če je torej velikost vzorca premajhna in porazdelitev prebivalstva ni normalna, z rezultatov ne moremo izračunati in meje napake ne bomo mogli najti.
Ustreznost in uporaba formule napake
Kadarkoli uporabimo vzorčne podatke za iskanje ustreznega odgovora za nabor prebivalstva, obstaja nekaj negotovosti in možnosti, da bi rezultat lahko odstopal od dejanskega rezultata. Mejna vrednost napake nam bo povedala, da je odsek vzorca odvisno od stopnje odstopanja. Moramo zmanjšati stopnjo napake, tako da naši vzorčni rezultati prikazujejo dejansko zgodbo s podatki o prebivalstvu. Torej nižja je stopnja napake, boljši bodo rezultati. Število napak dopolnjuje in dopolnjuje statistične podatke, ki jih imamo. Če na primer raziskava ugotovi, da 48% ljudi raje preživi čas doma med vikendom, ne moremo biti tako natančni in v teh podatkih je nekaj manjkajočih elementov. Ko smo tukaj uvedli mero napake, recimo 5%, bomo rezultat razlagali tako, da je 43-53% ljudem všeč ideja, da so med vikendom doma, kar ima popoln smisel.
Razlika napake Kalkulator formule
Uporabite lahko naslednji Kalkulator napake
| Z | |
| S | |
| √n | |
| Območje napake | |
| Območje napake | = |
|
|
Priporočeni članki
To je vodilo za formulo meje napake. Tukaj razpravljamo, kako izračunati mejo napake skupaj s praktičnimi primeri. Ponujamo vam tudi kalkulator Margin of Error s predlogo za excel, ki jo lahko naložite. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Vodnik po formuli amortizacije naravne črte
- Primeri formule časov podvojitve
- Kako izračunati amortizacijo?
- Formula za teorem o osrednji meji
- Altman Z ocena | Opredelitev | Primeri
- Formula amortizacije | Primeri s predlogo Excel