
Uvod v binomno porazdelitev v R
Ta članek opisuje, kako uporabiti binomne porazdelitve v R za nekaj operacij, povezanih s porazdelitvijo verjetnosti. Poslovna analiza uporablja binomno verjetnost za zapleten problem. R ima številne vgrajene funkcije za izračun binomskih porazdelitev, ki se uporabljajo pri statističnih interferencah. Binomna porazdelitev, znana tudi kot preskušanja Bernoullija, ima dve vrsti uspeha p in neuspeha S. Glavni cilj modela binomne porazdelitve je izračunati možne verjetnostne izide s spremljanjem določenega števila pozitivnih možnosti s ponovitvijo postopka določeno številokrat . Morali bi imeti dva možna rezultata (uspeh / neuspeh), zato je izid dihotomen. Vnaprej določeni matematični zapis je p = uspeh, q = 1-p.
Obstajajo štiri funkcije, povezane z porazdelitvijo binomov. So dbinom, pbinom, qbinom, rbinom. Spodaj je oblikovana sintaksa:
Sintaksa
- dbinom (x, velikost, težava)
- pbinom (x, velikost, težava)
- qbinom (x, velikost, težava) ali qbinom (x, velikost, težava, spodnja_razrednica, log_p)
- rbinom (x, velikost, težava)
Funkcija ima tri argumente: vrednost x je vektor kvantilov (od 0 do n), velikost je število poskusov sledi, prob označuje verjetnost za vsak poskus. Poglejmo enega za drugim s primerom.
1) dbinom ()
Je funkcija gostote ali porazdelitve. Vektorske vrednosti morajo biti celo število, ne smejo biti negativne številke. Ta funkcija poskuša najti številne uspehe v številki ne. preizkusov, ki so določeni.
Binomna porazdelitev prevzame velikost in x vrednosti. na primer velikost = 6, možne vrednosti x so 0, 1, 2, 3, 4, 5, 6, kar pomeni P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Izhod:
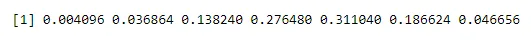
Izdelava verjetnosti ena
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Izhod:
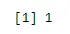
Primer 1 - bolnišnična baza podatkov kaže, da 65% bolnikov zboli za rakom. Kolikšna bo verjetnost, da bo 5 naključno izbranih pacientov, od katerih bodo 3 okrevali?
Tukaj uporabimo funkcijo dbinom. Verjetnost, da se bo 3 opomoglo s porazdelitvijo gostote na vseh točkah.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Izhod:

Za vrednost x od 0 do 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Izhod:
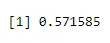
Nato ustvarite vzorec 40 papirjev in povečajte za 2, ustvarite tudi binomno s pomočjo dbinoma.
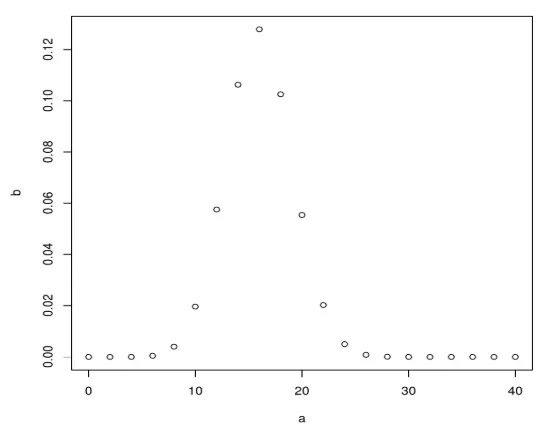
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Po izvedbi zgornje kode ustvari naslednji izhod. Binomna porazdelitev je prikazana s pomočjo plot () funkcije.
Primer 2 - Razmislimo o scenariju, predpostavimo, da je verjetnost, da bo študent izposodil knjigo iz knjižnice, 0, 7. V knjižnici je 6 študentov, kolikšna je verjetnost, da bodo trije izposodili knjigo?
tukaj P (X = 3)
Koda:
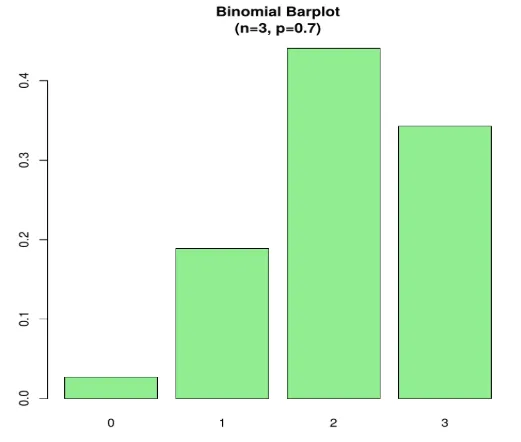
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Spodaj je prikazano, ko je p> 0, 5, torej je binomna porazdelitev pozitivno nagnjena kot prikazana.
Izhod:
2) Pbinom ()
izračuna kumulativne verjetnosti binomskih ali CDF (P (X <= x)).
Primer 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Izhod:

Primer 2: Dravid na 20% svojih poskusov, ko se keglje, doseže vilico. Če se 5-krat pokloni, kakšna bi bila verjetnost, da bo dosegel 4 ali manj vitice?
Verjetnost uspeha je tukaj 0, 2 in med 5 poskusi smo dobili
pbinom(4, size=5, prob=.2)
Izhod:
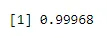
Primer 3: 4% Američanov je črncev. Poiščite verjetnost 2 črnih študentov, če naključno izberete 6 učencev iz razreda 100 brez zamenjave.
Ko je R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Izhod: -
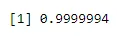
3) qbinom ()
To je kvantna funkcija in deluje obratno od funkcije kumulativne verjetnosti. Kumulativna vrednost se ujema z verjetnostno vrednostjo.
Primer: Koliko repov bo verjetno 0, 2, ko kovanec vržejo 61-krat.
a <- qbinom(0.2, 61, 1/2)
print(a)
Izhod: -
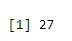
4) rbinom ()
Ustvari naključna števila. Različni rezultati prinašajo različne naključne rezultate, uporabljene v procesu simulacije.
Primer: -
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Izhod: -

Vsakič, ko ga izvršimo, daje naključne rezultate.
rbinom(200, 4, 0.4)
Izhod: -

Tukaj to storimo tako, da ob enem poskusu predpostavimo izid 30 prevratov kovancev.
rbinom(30, 1, 0.5)
Izhod: -
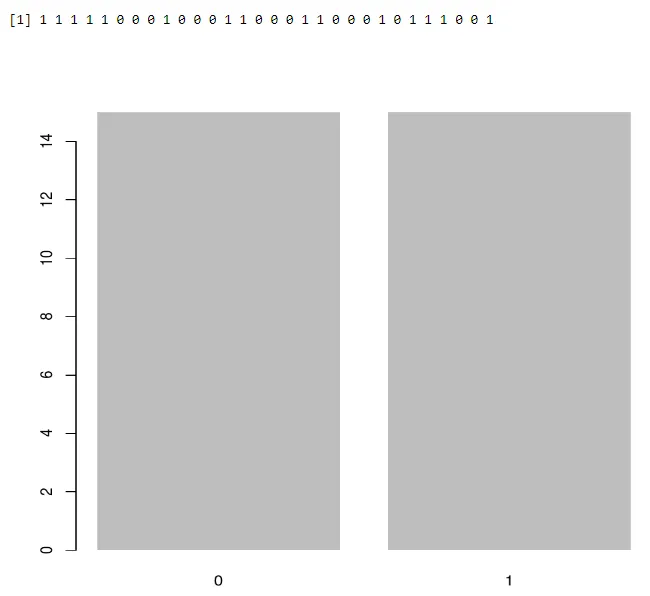
Uporaba barplota:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Izhod: -
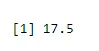
Da bi našli sredo uspeha
output <-rbinom(10, size=60, 0.3)
mean(output)
Izhod: -
Zaključek - Binomna porazdelitev v R
Zato smo v tem dokumentu obravnavali binomno porazdelitev v R. Simulirali smo s pomočjo različnih primerov v R studiu in R odrezkih ter opisali tudi vgrajene funkcije, ki pomagajo pri generiranju binomnih izračunov. Izračun binomne porazdelitve v R uporablja statistične izračune. Zato binomna porazdelitev pomaga pri iskanju verjetnosti in naključnem iskanju z uporabo binomske spremenljivke.
Priporočeni članki
To je priročnik za Binomno porazdelitev v R. Tu smo razpravljali o uvodu in njegovih funkcijah, povezanih s porazdelitvijo binomov, skupaj s skladnjo in ustreznimi primeri. Če želite izvedeti več, lahko preberete tudi druge naše predlagane članke -
- Formula binomne porazdelitve
- Ekonomija v primerjavi s podjetjem
- Tehnike poslovne analitike
- Linux distribucije