
Uvod v algoritem DFS
DFS je znan kot algoritem globine prvega iskanja, ki omogoča korake za prečkanje vsakega vozlišča grafikona, ne da bi pri tem ponovil nobeno vozlišče. Ta algoritem je enak globini prvega prečkanja drevesa, vendar se razlikuje v vzdrževanju logičnega signala, da preveri, ali je vozlišče že obiskano ali ne. To je pomembno za prečkanje grafa, saj v grafu obstajajo tudi cikli. V tem algoritmu se vzdržuje sklad za shranjevanje suspendiranih vozlišč med prečkanjem. Poimenovana je tako, ker najprej potujemo v globino vsakega sosednjega vozlišča in nato nadaljujemo s prečkanjem drugega sosednjega vozlišča.
Pojasnite algoritem DFS
Ta algoritem je v nasprotju z algoritmom BFS, kjer se obiskujejo vsa sosednja vozlišča, ki jim sledijo sosedje do sosednjih vozlišč. Graf začne z raziskovanjem grafa iz enega vozlišča in raziskuje njegovo globino pred povratnim sledenjem. V tem algoritmu sta upoštevani dve stvari:
- Obisk vrha : izbira točki ali vozlišča grafikona za prečkanje.
- Raziskovanje točke: prečkanje vseh vozlišč ob tej točki.
Prvo psevdo kodo za globino :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linearna prečka obstaja tudi za DFS, ki se lahko izvaja na 3 načine:
- Prednaročilo
- Naročilo
- PostOrder
Obrnjena postorder je zelo koristen način za prečkanje in se uporablja pri topološkem razvrščanju, pa tudi pri različnih analizah. Sklad se vzdržuje tudi za shranjevanje vozlišč, katerih raziskovanje še čaka.
Prehod grafikona v DFS
V DFS-ju sledimo spodnjim korakom za prečkanje grafa. Na primer, dani graf začnemo s prečkanjem od 1:
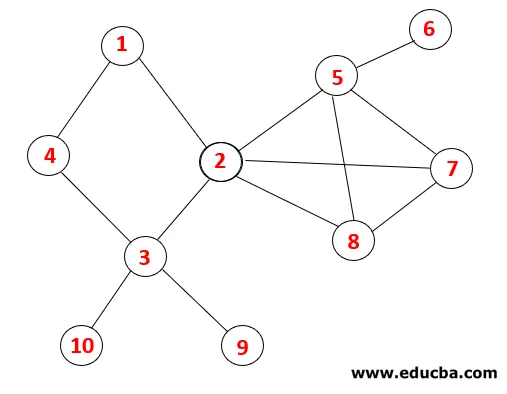
| Zložite | Prehodna zaporedje | Spanning Drevo |
| 1 |  |
|
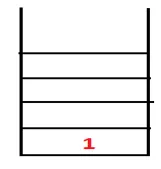 | 1, 4 |  |
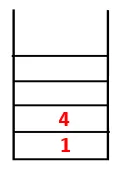 | 1, 4, 3 |  |
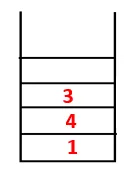 | 1, 4, 3, 10 | 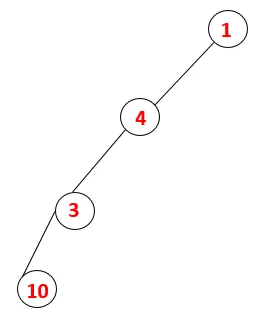 |
 | 1, 4, 3, 10, 9 | 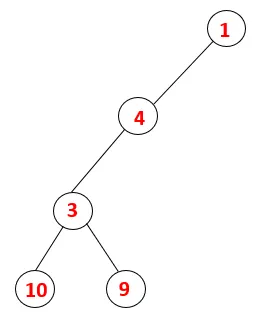 |
 | 1, 4, 3, 10, 9, 2 | 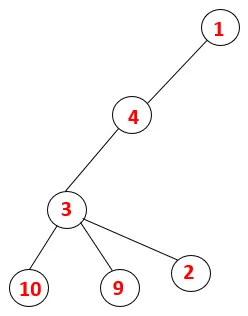 |
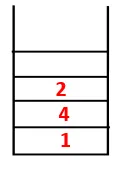 | 1, 4, 3, 10, 9, 2, 8 |  |
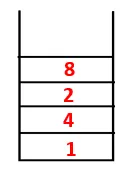 | 1, 4, 3, 10, 9, 2, 8, 7 | 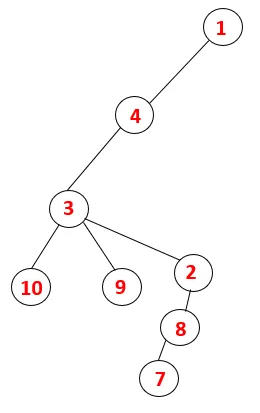 |
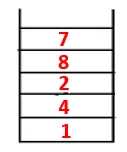 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
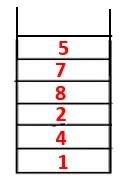 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 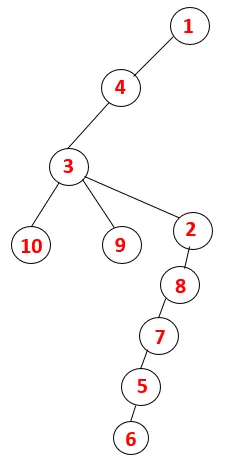 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 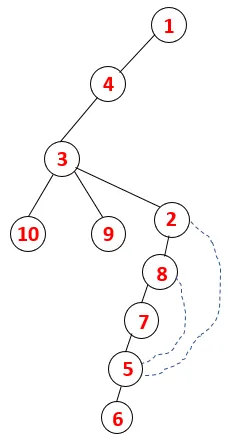 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
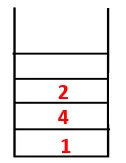 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 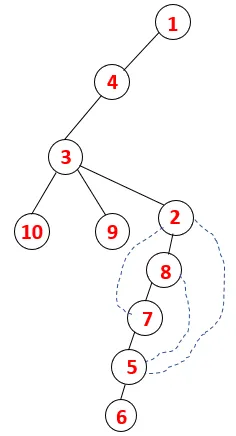 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 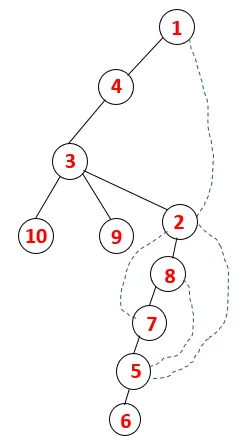 |
Pojasnilo algoritma DFS
Spodaj so koraki do algoritma DFS s prednostmi in slabostmi:
1. korak: Obisk vozlišča 1 je dodan v zaporedje in v drevo.
2. korak: Raziskani so sosednji vozlišči 1, to je 4, zato 1 potisnemo na zlaganje in 4 potisnemo v zaporedje, kot tudi vpeto drevo.
Korak 3: Eno od sosednjih vozlišč 4 je raziskano in tako 4 potisnemo v kup, 3 pa v drevo in zaporedje.
4. korak: Sosednja 3 vozlišča raziskujemo tako, da jih potisnemo na sklad in 10 vstopi v zaporedje. Ker ni sosednjega vozlišča do 10, tako 3 izskoči iz sklada.
5. korak: Raziskujemo še eno sosednje vozlišče 3 in 3 potisnemo na kup in 9 obiščemo. Nobeno sosednje vozlišče 9, torej 3, je izpuščeno in obiskano je zadnje sosednje vozlišče 3, tj. 2.
Podoben postopek sledimo vsem vozliščem, dokler se sklad ne izprazni, kar kaže na stanje ustavitve algoritma za prečkanje. - -> pikčaste črte v razporednem drevesu se nanašajo na zadnje robove, ki so na grafu.
Na ta način se prečkajo vsa vozlišča v grafu, ne da bi se katero od vozlišč ponovilo.
Prednosti in slabosti
- Prednosti: Te potrebe po pomnilniku za ta algoritem so zelo manjše. Manjša prostorska in časovna zahtevnost kot BFS.
- Slabosti: rešitev ni zajamčena. Topološko razvrščanje. Iskanje mostov grafa.
Primer za implementacijo algoritma DFS
Spodaj je primer za implementacijo algoritma DFS:
Koda:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Izhod:
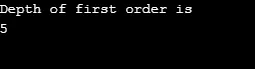
Pojasnilo zgornjemu programu: Naredili smo graf s 5 točki (0, 1, 2, 3, 4) in uporabili obiskano matriko za sledenje vseh obiskanih vertik. Nato se za vsako vozlišče, katerega sosednja vozlišča obstajajo, enak algoritem ponavlja, dokler niso obiskana vsa vozlišča. Nato se algoritem vrne v klicanje klicev in ga prikaže iz sklada.
Zaključek
Zahteva tega grafikona za pomnilnik je manjša v primerjavi z BFS, saj je za vzdrževanje potreben samo en sklad. Rezultat je DFS vpeto drevo in prečno zaporedje, vendar nista konstantna. Možno je več zaporednih prehodov glede na izbrano vrhovo in raziskovanje.
Priporočeni članki
To je vodnik po algoritmu DFS. Tukaj razpravljamo po korakih o razlagi, prečkamo graf v tabeli s prednostmi in slabostmi. Obiščite lahko tudi druge naše sorodne članke, če želite izvedeti več -
- Kaj je HDFS?
- Algoritmi poglobljenega učenja
- Ukazi HDFS
- Algoritem SHA