
Koeficient formule za določanje (vsebina)
- Formula
- Primeri
Kakšen je koeficient formule določanja?
V statistiki je koeficient določitve, imenovan tudi R2, orodje, ki določa in ocenjuje sposobnost statističnega modela za razlago in napovedovanje prihodnjih rezultatov. Z drugimi besedami, če imamo v modelu odvisno spremenljivko y in neodvisno spremenljivko x, potem R 2 pomaga pri določanju variacije y z variacijo x. Je eden ključnih rezultatov regresijske analize in se uporablja, kadar želimo napovedati prihodnost ali testirati nekatere modele s sorodnimi informacijami. Vrednost R2 je med 0 in 1 in višja je vrednost R 2, boljši bosta napoved in moč modela. R2 je zelo podoben korelacijskemu koeficientu, saj korelacijski koeficient meri neposredno povezavo dveh spremenljivk. R2 je v bistvu kvadrat korelacijskega koeficienta.
Formula za koeficient določitve:
Za izračun koeficienta določitve obstaja več formul:
- Uporaba korelacijskega koeficienta:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Kje:
- X - Podatkovne točke v podatkovnem nizu X
- Y - Podatkovne točke v podatkovnem nizu Y
- X m - povprečje nabora podatkov X
- Y m - povprečje podatkovnega niza Y
Torej
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Uporaba regresijskih izhodov
Koeficient določitve (R 2 ) = Pojasnjena variacija / Skupna variacija
Koeficient določitve (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Kje:
- TSS - Skupni seštevek kvadratov = Σ (Yi - Ym) 2
- MSS - Vsota vzorcev kvadratov = Σ (Y - Ym) 2
- RSS - Preostala vsota kvadratov = Σ (Yi - Y ^) 2
Y je predvidena vrednost modela, Yi je i vrednost, Ym pa srednja vrednost
Primeri koeficienta formule določitve (s predlogo Excel)
Vzemimo primer, da bolje razumemo izračun koeficienta določitve.
Ta koeficient predloge Excel Formula Excel lahko prenesete tukaj - Koeficient predloge Formula ExcelKoeficient formule za določanje - Primer 1
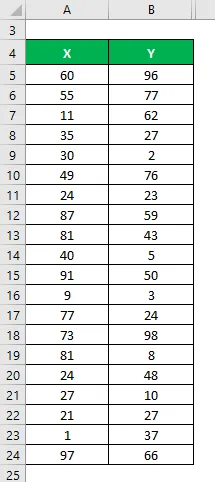
Recimo, da imamo dva podatkovna niza X&Y in vsak vsebuje 20 naključnih podatkovnih točk. Izračunajte koeficient določitve za niz podatkov X & Y.
Srednja vrednost se izračuna kot:
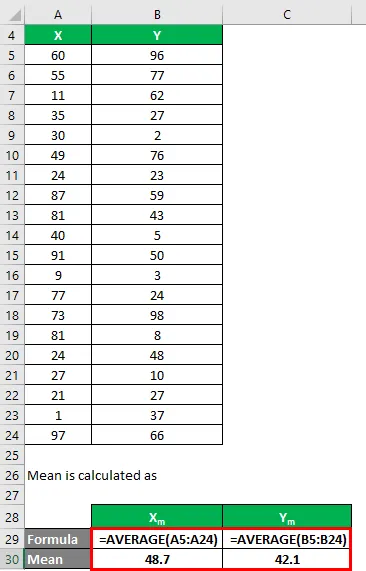
- Srednja vrednost nabora podatkov X = 48, 7
- Srednja vrednost nabora podatkov Y = 42.1
Zdaj moramo izračunati razliko med podatkovnimi točkami in srednjo vrednostjo.
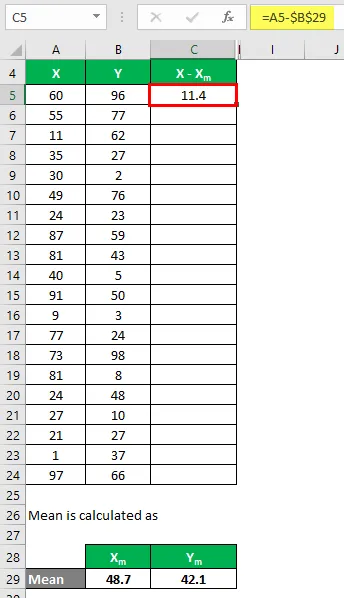
Podobno izračunajte za vse podatke X.
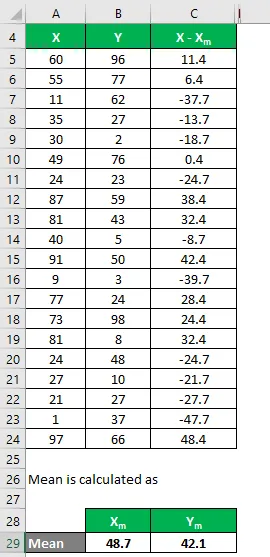
Podobno izračunajte tudi za niz Y.

Izračunajte kvadrat razlike za oba niza podatkov X in Y.
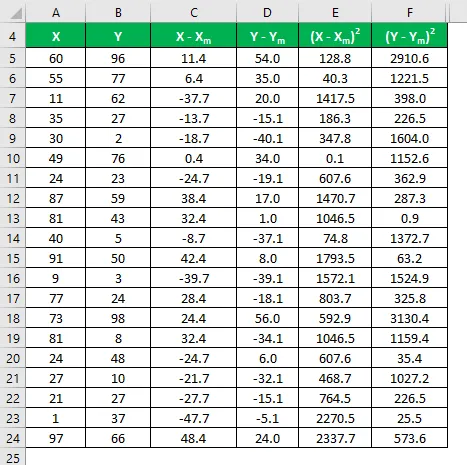
Pomnožite razliko v X z Y.
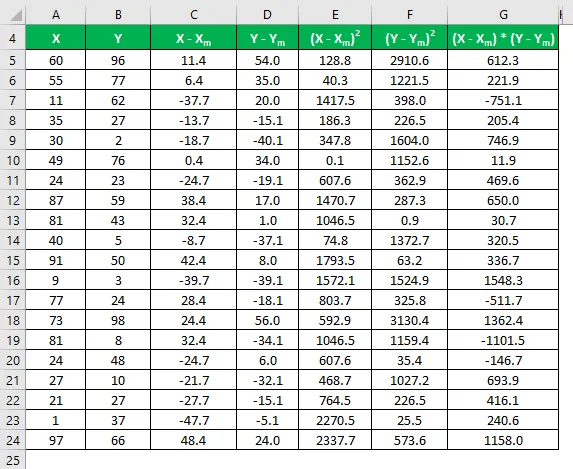
Korelacijski koeficient se izračuna po spodnji formuli
Korelacijski koeficient = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
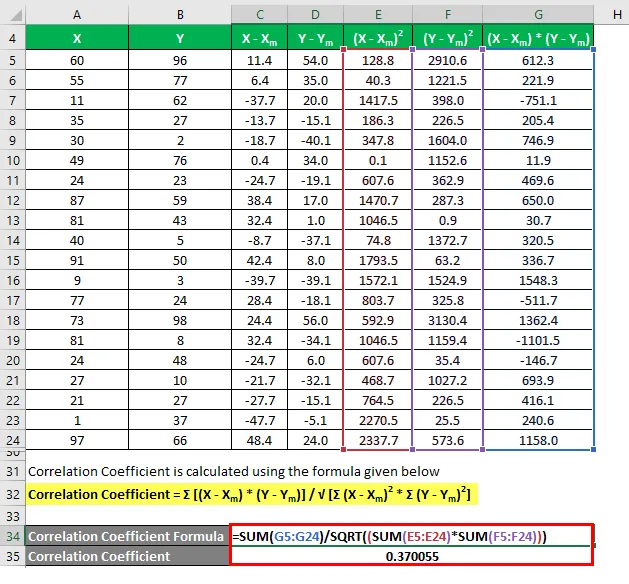
Koeficient določitve se izračuna po spodnji formuli
Koeficient določitve = (korelacijski koeficient) 2
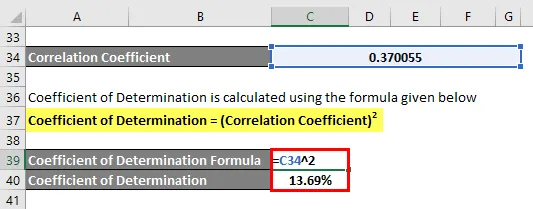
Koeficient določitve = 13, 69%
Koeficient formule za določanje - primer # 2
Recimo, da ste zelo naklonjen vlagatelju in želite vložiti denar na delnico. Niste prepričani, v katere zaloge bi vlagali in tudi vaš apetit za tveganje je nizek. Torej želite vlagati v zaloge, ki so varne in lahko posnemajo uspešnost indeksa. Vaš prijatelj, ki je aktivni vlagatelj, je za vas na podlagi njihovih temeljnih in tehničnih informacij uvrstil 3 zaloge in želite izbrati 2 delnici med temi tremi.
Zbrali ste tudi podatke o njihovih zgodovinskih poročilih v zadnjih 15 letih.
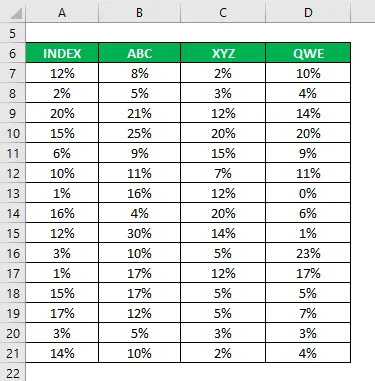
Korelacijski koeficient se izračuna po formuli excel
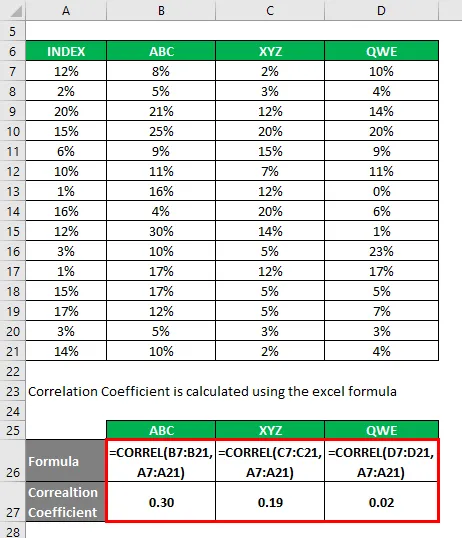
Koeficient določitve se izračuna po spodnji formuli
Koeficient določitve = (korelacijski koeficient) 2
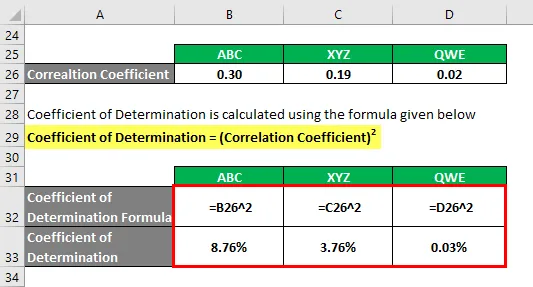
Na podlagi informacij boste izbrali zaloge ABC in XYZ, ki jih boste investirali, saj imajo najvišji koeficient določitve.
Pojasnilo
Kot je razloženo zgoraj, je koeficient določitve kvadrat korelacije med dvema naboroma podatkov. Če je R2 0, to pomeni, da ni korelacije in neodvisna spremenljivka ne more predvideti vrednosti odvisne spremenljivke. Podobno, če je njegova vrednost 1, pomeni, da bo neodvisna spremenljivka vedno uspešna pri napovedovanju odvisne spremenljivke. Obstajajo pa tudi nekatere omejitve. Čeprav nam pove korelacijo med dvema naboroma podatkov, nam ne pove, ali je ta vrednost dovolj ali ne.
Prav tako velika vrednost R2 ne pomeni vedno, da imata dve spremenljivki močna razmerja in je lahko naključna. Na primer: Recimo, da je vrednost R 2 med številom avtomobilov, prodanih v enem letu, in številom prodanih škatel za sladoled v enem letu 80%. Toda med tema dvema ni nobene zveze. Med uporabo R2 je treba biti zelo previden in najprej razumeti podatke, nato pa uporabiti metodo
Ustreznost in uporaba koeficienta formule določanja
Obstaja veliko praktičnih aplikacij R 2 . Na primer, vlagatelje R2 pogosto uporabljajo, da primerjajo uspešnost svojega portfelja s trgom in poskušajo napovedati tudi prihodnje smeri. Podobno tudi hedge skladi R2 pomagajo pri modeliranju tveganja v svojih modelih. Toda na koncu rezultat temelji na čistih številkah in statistikah, ki so včasih lahko zavajajoče. Kot že omenjeno, je treba najprej preveriti, ali je izhod R2 smiseln v resničnem življenju.
Priporočeni članki
To je vodnik za Koeficient formule določitve. Tukaj razpravljamo o tem, kako izračunati koeficient določitve skupaj s praktičnimi primeri in naložljivo predlogo Excela. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Vodnik po formuli za tržno tveganje Premium
- Primeri formule razmerja pokritja
- Kalkulator za formulo stroškov na osnovi aktivnosti
- Kako izračunati razmerje informacij s formulo?