Uvod v hierarhični algoritem grozdov
Hierarhični algoritem združevanja je nenadzorovana tehnika strojnega učenja. Njegov cilj je poiskati naravno združevanje na podlagi značilnosti podatkov.
Namen algoritma hierarhičnega združevanja je najti gnezdene skupine podatkov z gradnjo hierarhije. Podobno je z biološko taksonomijo rastlinskega ali živalskega kraljestva. Hierarhični grozdi so na splošno predstavljeni z uporabo hierarhičnega drevesa, znanega kot dendrogram.
Vrste algoritma hierarhičnega grozda
Hierarhični algoritmi združevanja so 2 tipa:
- Delljiv
- Aglomerative
1. deliti
To je pristop od zgoraj navzdol, kjer sprva celotne podatke obravnava kot eno skupino, nato pa podatke iterativno razdeli na podskupine. Če je znano število algoritma hierarhičnega združevanja, potem se postopek delitve ustavi, ko je doseženo število grozdov. Drugače se postopek ustavi, ko se podatki ne morejo več deliti, kar pomeni, da je podskupina, pridobljena s trenutno iteracijo, enaka tisti, ki je bila pridobljena iz prejšnje iteracije (lahko tudi upoštevamo, da se delitev ustavi, ko je vsaka podatkovna točka grozd. ).
2. aglomerative
Gre za pristop od spodaj navzgor, ki temelji na združevanju grozdov. Sprva se podatki razdelijo na m enotonske grozde (kjer je vrednost m število vzorcev / podatkovnih točk). Dva grozda sta združena v en iterativno, kar zmanjša število grozdov v vsaki ponovitvi. Ta postopek združevanja grozdov se ustavi, ko so vsi grozdi združeni v eno ali je doseženo število želenih grozdov.
Na 1. stopnji so m grozdi, ki se na ravni m zmanjšajo na 1 grozd. Tiste podatkovne točke, ki se združijo in tvorijo grozd na nižji ravni, ostanejo v istem grozdu tudi na višjih nivojih. Recimo, da obstaja 8 točk x1..x8, torej na začetku je 8 skupin na 1. ravni. Recimo, da se točki x1 in x2 združita v skupino na ravni 2, nato pa do ravni 8 ostaneta v isti skupini.
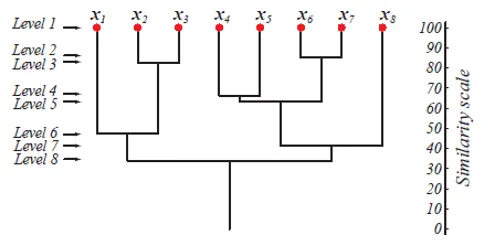
Zgornja slika prikazuje dendrogramski pristop kloniranja aglomeracije za 8 podatkovnih točk in lestvico podobnosti, ki ustreza vsaki ravni.
Ravni grozdov nam dajo predstavo o tem, kako podobne so podatkovne točke v grozdih. Kot je prikazano na sliki 1, se prej podatkovne točke združijo v gručo, podobne so. Torej so podatkovne točke v grozdu na ravni 2 (npr. X2 in x3) bolj podobne kot podatkovne točke v gruči na ravni 6 (npr. X1 in x2).
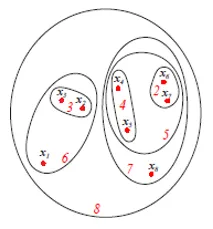
Na zgornji sliki je prikazan Set ali Venn diagram, ki prikazuje aglomerativni pristop združevanja zgoraj omenjenih 8 podatkovnih točk. Za združevanje lahko uporabimo tako dendrograme kot nastavljene predstavitve. Vendar je ponavadi prednostni prikaz dendrograma zastopanje sredstev ne more količinsko predstaviti podobnosti grozda.
Koraki za hierarhični algoritem grozdov
Upoštevajte naslednje korake za algoritem hierarhičnega združevanja, ki je dan spodaj:
1. Algoritem
Aglomerativni hierarhični algoritem združevanja
- Začnite inicializirati c, c1 = n, Di = (xi), i = 1, …, n '
- Naredi c1 = c1 - 1
- Poiščite najbližje skupine, recimo Di in Dj
- Spojite Di in Dj
- Dokler c = c1
- Vrni c grozde
- Konec
Ta algoritem se začne najprej z nimi grozdi, kjer je vsaka podatkovna točka grozd. Z vsako ponovitvijo se število gruč zmanjša za 1, ko se združijo dve najbližji grozdi. Ta postopek se nadaljuje, dokler se število gruč ne zmanjša na vnaprej določeno vrednost c.
Kako se odločiti, kateri grozdi so v bližini?
To je določeno z uporabo več meritev razdalje, ki so naslednje:
- Najmanjša razdalja med grozdi dmin (Di, Dj). Koristno za samske.
- Največja razdalja med grozdi dmax (Di, Dj). Koristno za dokončanje.
- Povprečna razdalja med grozdiv davg (Di, Dj).
Kaj je enojna povezava in popolna povezava?
- Kadar se dmin (di, dj) uporablja za iskanje razdalje med dvema skupinama in algoritem preneha, če razdalja med najbližjimi skupinami presega prag, potem se algoritem imenuje en sam algoritem povezave.
- Kadar se dmax (Di, Dj) uporablja za iskanje razdalje med dvema skupinama in algoritem preneha, če razdalja med najbližjimi skupinami presega prag, potem se algoritem imenuje celoten algoritem povezave.
- Upoštevajmo vsako podatkovno točko kot vozlišče grafa. Med dvema podatkovnima točkama je rob, če pripadata istemu grozdu. Ko sta dve najbližji grozdi združeni, se doda rob. Imenuje se ena povezava, ker obstaja edinstvena pot od enega vozlišča do drugega.
- Algoritem popolne povezave združuje dve grozdi tako, da zmanjša razdaljo med dvema najbolj oddaljenima točkama.
- En algoritem povezave ustvari raztezno drevo. Vendar je ta algoritem občutljiv na hrup. Popolni algoritem povezave ustvari celoten graf.
Kakšna je časovna zapletenost algoritma?
Recimo, da imamo n d-dimenzionalnega prostora n vzorcev, za oblikovanje c skupin pa uporabljamo dmin (Di, Dj). Izračunati moramo n (n - 1) razmikov med točkami - od katerih je vsak izračun O (d 2 ) - in rezultate vstaviti v tabelo razmikov med točkami. Kompleksnost prostora je O (n 2 ). Iskanje para najmanjše razdalje (za prvo združitev) zahteva, da stopimo skozi celoten seznam in pri tem upoštevamo indeks najmanjše razdalje.
Tako je za prvi aglomerativni korak zapletenost O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Za drug poljuben korak aglomeracije (tj. Od c1 do c1 - 1) zgolj stopimo skozi n (n - 1) - c1 "neuporabljene" razdalje na seznamu in najdemo najmanjšo, za katero x in x 'ležita v različnih grozdih . To je spet O (n (n − 1) −c1). Skupna časovna zahtevnost je torej O (cn 2 d 2 ), v značilnih pogojih pa n >> c.
2. Vizualizacija
Ko se podatki razdelijo v grozde, je dobra praksa, da grozde vizualiziramo, da dobimo predstavo o tem, kako izgleda združevanje. Toda vizualizacija teh podatkov o velikih dimenzijah je težavna. Zato uporabljamo analizo glavnih komponent (PCA) za vizualizacijo. Po PCA dobimo podatkovne točke v prostoru z majhnimi dimenzijami (na splošno 2D ali 3D), ki ga lahko oblikujemo, da vidimo skupino.
Opomba: Velika dimenzija pomeni veliko število funkcij in ne število podatkovnih točk.3. Vrednotenje
Eden od načinov za ocenjevanje grozdov je, da mora biti razdalja točk med grozdi (razdalja med gručami) veliko večja kot razdalja točk znotraj grozda (razdalja znotraj skupine).
Zaključek
Sledi nekaj ključnih ukrepov:
- Hierarhični algoritem združevanja se uporablja za iskanje ugnezdenih vzorcev v podatkih
- Hierarhično združevanje je dveh vrst - delitveno in aglomerativno
- Dendrogram in set / Venn diagram lahko uporabimo za predstavitev
- Enojna povezava združi dve grozdi tako, da zmanjša minimalno razdaljo med njima. Tvori razpon
- Popolna povezava združi dva grozda z zmanjšanjem največje razdalje med tvori celoten graf.
- Skupna časovna zapletenost algoritma hierarhičnega združevanja je O (cn 2 d 2 ), kjer je c vnaprej določeno število grozdov, n je število vzorcev in d je dvodimenzionalni prostor n vzorcev.
Priporočeni članki
To je vodnik po algoritmu Hierarhična gruča. Tukaj razpravljamo o tipih in korakih algoritmov hierarhičnega združevanja. Če želite izvedeti več, si oglejte tudi naslednje članke -
- Hierarhična analiza grozdov
- Hierarhična gruča v R '
- Algoritem grozda
- Kaj je združevanje v podatkovno rudarjenje?
- Hierarhična gruča | Aglomerativno in delitveno grozdenje
- C ++ algoritem | Primeri algoritma C ++