Uvod v hierarhično grozdenje
- Pred kratkim je ena od naših strank prosila našo ekipo, da pripravi seznam segmentov po vrstnem redu po meri svojih strank, da jih usmeri v franšizo enega od svojih novo predstavljenih izdelkov. Jasno je, da samo segmentiranje kupcev z delnim združevanjem (k-pomeni, c-fuzzy) ne bo prineslo pomembnega vrstnega reda, kjer pride na vrsto hierarhično združevanje.
- Hierarhično združevanje podatkov ločuje podatke v različne skupine na podlagi nekaterih ukrepov podobnosti, znanih kot grozdi, ki v bistvu ciljajo na gradnjo hierarhije med grozdi. V osnovi je nenadzorovano učenje in izbira lastnosti za merjenje podobnosti je specifična za uporabo.
Grozd hierarhije podatkov
- Aglomerativno grozdenje
- Delitveno grozdanje
Vzemimo primer podatkov, ocen, ki jih je dobilo 5 učencev, da jih bomo razvrstili za prihajajoče tekmovanje.
| Študent | Oznake |
| A | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35-ih |
1. Aglomerativna gruča
- Za začetek štejemo vsako težo posameznih točk / elementov kot grozde in nadaljujemo z združevanjem podobnih točk / elementov, da tvorimo novo gručo na novi ravni, dokler nam ne ostane en sam grozd, je pristop od spodaj navzgor.
- Posamezna in popolna povezava sta dva priljubljena primera aglomeracijskega združevanja. Razen povprečne in Centroidne povezave. V enojni povezavi na vsakem koraku združimo dva grozda, katerih dva najbližja člana imata najmanjšo razdaljo. V popolni povezavi se združimo v člane najmanjše razdalje, ki zagotavljajo najmanjšo največjo dvojno razdaljo.
- Matrica bližine, Je jedro za izvajanje hierarhičnega združevanja, ki daje razdaljo med posameznimi točkami.
- Naredimo matrico bližine za naše podatke, podane v tabeli, saj izračunamo razdaljo med posameznimi točkami z drugimi točkami, bo to asimetrična matrika oblike n × n, v našem primeru 5 × 5 matric.
Priljubljena metoda za izračun razdalje je:
- Euklidijska razdalja (v kvadratu)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattna razdalja
dist((x, y), (a, b)) =|x−c|+|y−d|
Najpogosteje se uporablja evklidska razdalja, tu bomo uporabili isto in šli bomo s kompleksno povezavo.
| Študent (grozdi) | A | B | C | D | E |
| A | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonalni elementi matrike bližine bodo vedno 0, saj bo razdalja med točko z isto točko vedno 0, torej so diagonalni elementi oproščeni razvrščanja.
Tukaj je v iteraciji 1 najmanjša razdalja 3, zato združimo A in B, da tvorimo gručo, znova oblikujemo novo matrico bližine z grozdom (A, B), tako da (A, B) odsekamo kot 10, tj. Največ ( 7, 10) tako bi bila na novo oblikovana matrica bližine
| Grozdi | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
V iteraciji 2, 7 je najmanjša razdalja, zato združimo C in E, tvorimo novo gručo (C, E), ponavljamo postopek, ki je sledil v iteraciji 1, dokler ne končamo z enim grozdom, tu se ustavimo pri iteraciji 4.
Celoten postopek je prikazan na spodnji sliki:
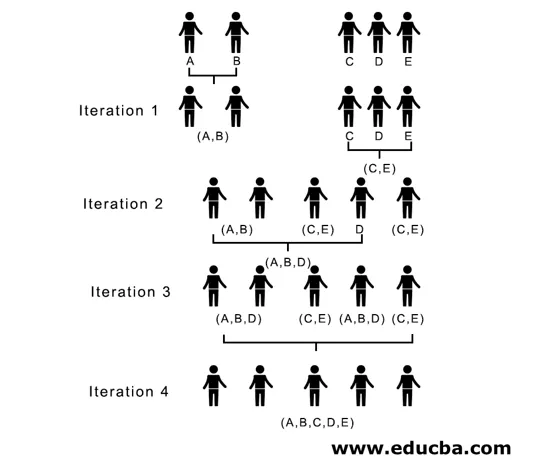
(A, B, D) in (D, E) sta dve grozdi, ki sta nastali pri iteraciji 3, pri zadnji iteraciji, ki jo vidimo, nam ostane en sam grozd.
2. Razdeljevanje grozdov
Za začetek štejemo vse točke kot en grozd in jih ločimo na najbolj oddaljeno razdaljo, dokler posamezne točke ne zaključimo kot posamezne grozde (ni nujno, da se lahko ustavimo na sredini, odvisno je od najmanjšega števila elementov, ki jih želimo v vsakem grozdu) na vsakem koraku. Je ravno nasprotno od strnjenega strnjevanja in je pristop od zgoraj navzdol. Delitveno združevanje je način, ki se ponavlja, k pomeni gručenje.
Izbira med aglomerativnim in delitvenim grozdom je spet odvisna od aplikacije, vendar je treba upoštevati nekaj točk:
- Divizijsko je bolj zapleteno kot aglomerativno grozdenje.
- Delitveno združevanje je učinkovitejše, če ne ustvarimo popolne hierarhije do posameznih podatkovnih točk.
- Aglomerativno združevanje sprejme odločitev z upoštevanjem lokalnih vzorcev, ne da bi pri tem upoštevali globalne vzorce, ki jih ni mogoče spremeniti.
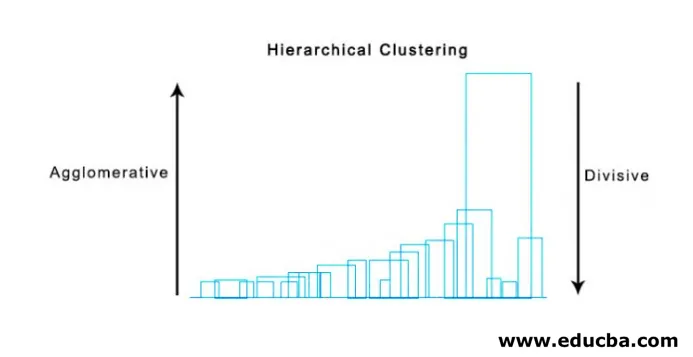
Vizualizacija hierarhične gruče
Super uporabna metoda za vizualizacijo hierarhičnega združevanja, ki pomaga pri poslovanju, je Dendogram. Dendogrami so drevesne strukture, ki beležijo zaporedje spajanj in razcepov, pri katerih navpična črta predstavlja razdaljo med grozdi, razdalja med navpičnimi črtami in razdalja med grozdi je neposredno sorazmerna, tj.
Z dendogramom lahko določimo število grozdov, na dendogramu narišemo črto, ki seka z najdaljšo navpično črto, število navpičnih premic, ki se sekajo, bo število gruč.
Spodaj je primer Dendogram.
Obstaja precej preprost in neposreden paket python in njegove funkcije za izvajanje hierarhičnega združevanja in narisovanja dendogramov.
- Hierarhija iz učenja.
- Cluster.hierarchy.dendogram za vizualizacijo.
Skupni scenariji, v katerih se uporabljajo hierarhične gruče
- Segmentacija kupcev na trženje izdelkov ali storitev.
- Načrt mesta za določitev krajev za gradnjo struktur / storitev / stavbe.
- Analiza družbenih omrežij na primer identificira vse oboževalce MS Dhonija, ki oglašujejo njegovo biografijo.
Prednosti hierarhične gruče
Prednosti so podane v nadaljevanju:
- V primeru delnega združevanja, kot so k-sredstva, je treba pred gručenjem poznati število gruč, kar v praktičnih aplikacijah ni mogoče, medtem ko pri hierarhičnem združevanju ni potrebno predhodno poznavanje števila grozdov.
- Hierarhično združevanje ustvarja hierarhijo, to je strukturo, ki je bolj informativna od nestrukturiranega niza ravnih grozdov, ki se vrne z delnim združevanjem.
- Hierarhično združevanje je enostavno izvajati.
- Prikaže večino scenarijev.
Zaključek
Vrsta združevanja ima velike razlike pri predstavitvi podatkov; Hierarhično združevanje, ki je bolj informativno in enostavno za analizo, je bolj prednostno kot delno združevanje. In pogosto je povezana s toplotnimi zemljevidi. Da ne pozabimo na atribute, izbrane za izračun podobnosti ali razlike, ki pretežno vplivajo tako na grozde kot na hierarhijo.
Priporočeni članki
To je vodnik po hierarhični grozdi. Tukaj razpravljamo o uvodu, prednostih hierarhičnih grozdov in skupnih scenarijih, v katerih se uporabljajo hierarhične gruče. Obiščite lahko tudi druge naše predlagane članke, če želite izvedeti več -
- Algoritem grozda
- Grozd v strojnem učenju
- Hierarhična gruča v R
- Metode grozdenja
- Kako odstraniti hierarhijo v Tableauu?