
Uvod v ANOVA v R
Naslednji članek ANOVA in R ponuja pregled primerjave srednje vrednosti različnih skupin. Analiza variacije (ANOVA) je zelo pogosta tehnika, ki se uporablja za primerjavo srednje vrednosti različnih skupin. Za testiranje hipotez se uporablja model ANOVA, kjer se za populacijo ustvari določena predpostavka ali parameter, statistična metoda pa se uporablja za določitev, ali je hipoteza resnična ali napačna.
Hipoteza izhaja iz domneve preiskovalca in razpoložljivih informacij o prebivalstvu. ANOVA se imenuje analiza variacije in se uporablja za preskušanje hipotez, kjer je treba meriti sredstva spremenljivke v več neodvisnih skupinah.
Na primer, v laboratoriju za preučevanje ali izumljanje novega zdravila za debelost bodo raziskovalci primerjali rezultat eksperimentalnega in standardnega zdravljenja. V študiji debelosti je mogoče pridobiti dragocene rezultate, če lahko povprečno stopnjo debelosti prebivalstva primerjamo v različnih starostnih skupinah. V tem primeru bi radi opazovali povprečno stopnjo debelosti med različnimi starostnimi skupinami, kot so starost (5 do 18), (19, 35) in (36 do 50). Metoda ANOVA se uporablja, ker obstajata več kot dve skupini, ki sta neodvisni. Za primerjavo povprečne debelosti neodvisnih skupin se uporablja metoda ANOVA. Uporablja se funkcija aov () in sintaksa je aov (formula, podatki = podatkovni okvir) V tem članku bomo spoznali model ANOVA in nadalje obravnavali enosmerni in dvosmerni model ANOVA skupaj s primeri.
Zakaj ANOVA?
- Ta tehnika se uporablja za odgovor na hipotezo ob analizi več skupin podatkov. Statističnih pristopov je več, vendar se ANOVA v R uporablja, kadar je treba primerjati več kot dve neodvisni skupini, kot v našem prejšnjem primeru tri različne starostne skupine.
- Tehnika ANOVA meri srednjo vrednost neodvisnih skupin, da raziskovalcem omogoči rezultat hipoteze. Za natančne rezultate je treba upoštevati vzorčna sredstva, velikost vzorca in standardni odmik od vsake posamezne skupine.
- Za primerjavo je mogoče opazovati povprečno vrednost za vsako od treh skupin. Vendar ima ta pristop omejitve in se lahko izkaže za napačen, ker te tri primerjave ne upoštevajo skupnih podatkov in tako lahko vodijo do napake tipa 1. R nam daje funkcijo za izvedbo analize ANOVA, da preučimo spremenljivost med neodvisnimi skupinami podatkov. Obstaja pet stopenj izvajanja analize ANOVA. V prvi fazi so podatki razporejeni v formatu csv in stolpec se ustvari za vsako spremenljivko. Eden od stolpcev bi bil odvisna spremenljivka, preostali pa neodvisna spremenljivka. Na drugi stopnji se podatki preberejo v studiu R in jih ustrezno poimenujejo. Na tretji stopnji je nabor podatkov pritrjen na posamezne spremenljivke in jih bere pomnilnik. Končno je ANOVA v R opredeljena in analizirana. V spodnjih razdelkih sem navedel nekaj primerov študije primerov, v katerih je treba uporabiti tehnike ANOVA.
- Na 12 njivah so testirali šest insekticidov, raziskovalci pa so prešteli število hroščev, ki so ostali na vsakem polju. Kmetiji morajo zdaj vedeti, ali so insekticidi kaj pomembni, in če je odgovor, kateri od njih najbolje uporabljajo. Na to vprašanje odgovorite s funkcijo aov () za izvedbo ANOVA.
- Petdeset bolnikov je prejelo eno od petih zdravil za zmanjšanje holesterola (trt). Tri od pogojev zdravljenja so vključevala isto zdravilo, ki je bilo dano kot 20 mg enkrat na dan (1-krat) 10 mg dvakrat na dan (2-krat) 5 mg štirikrat na dan (4-krat). Dva preostala stanja (drugD in drogaE) sta predstavljala konkurenčna zdravila. Katero zdravljenje z zdravili je povzročilo največje znižanje holesterola (odziv)?
ANOVA enosmerna
- Enosmerna metoda je ena od osnovnih metod ANOVA, pri kateri se uporablja analiza variacije in primerja povprečna vrednost več skupin prebivalstva.
- Enosmerna ANOVA je dobila ime zaradi razpoložljivosti enosmernih tajnih podatkov. V enosmerni ANOVA spremenljivki in ena ali več neodvisnih spremenljivk so lahko na voljo.
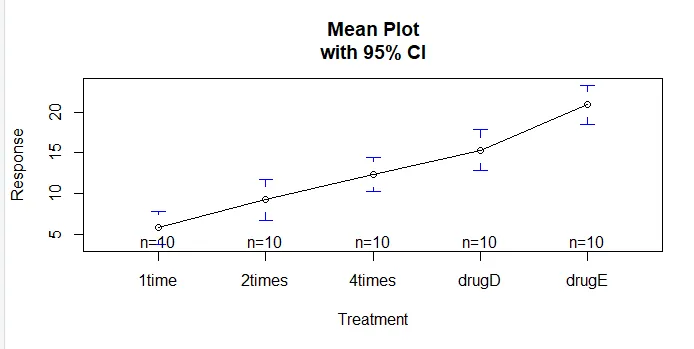
- Na primer, izvedli bomo tehniko ANOVA na nizu podatkov o holesterolu. Nabor podatkov je sestavljen iz dveh spremenljivk trt (ki sta obravnavani na 5 različnih ravneh) in spremenljivk odziva. Neodvisna spremenljivka - skupine zdravljenja z zdravili, odvisna spremenljivka - pomeni 2 ali več skupin ANOVA. Iz teh rezultatov lahko potrdite, da je bil odmerek 5 mg 4-krat na dan boljši od jemanja odmerka dvajset mg enkrat na dan. Zdravilo D ima boljše učinke v primerjavi z zdravilom E
Zdravilo D zagotavlja boljše rezultate, če ga jemljemo v odmerkih 20 mg v primerjavi z zdravilom E
V paketu multicomp uporablja nabor podatkov o holesteroluinstall.packages('multcomp')
library(multcomp)
str(cholesterol)
attach(cholesterol)
aov_model <- aov(response ~ trt)
Test ANOVA F za zdravljenje (trt) je pomemben (p <.0001), kar dokazuje, da je pet zdravljenj
# niso vsi enako učinkoviti.
povzetek (aov_model)
odvajanje (holesterol)

Funkcijo plotmeans () v paketu gplots je mogoče uporabiti za izdelavo grafa skupinskih sredstev in njihovih intervalov zaupanja. To jasno kaže razlike v zdravljenjuinstall.packages('gplots')
library(gplots)
plotmeans(response ~ trt, xlab="Treatment", ylab="Response",
main="Mean Plot\nwith 95% CI")
Preučimo izhod iz TukeyHSD () za parne razlike med sredstvi skupine
TukeyHSD (aov_model)
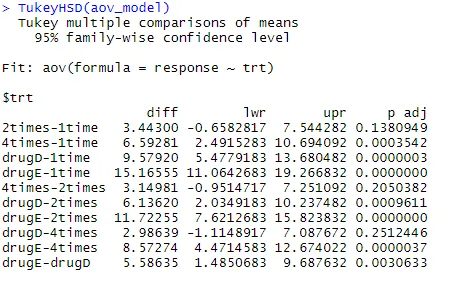
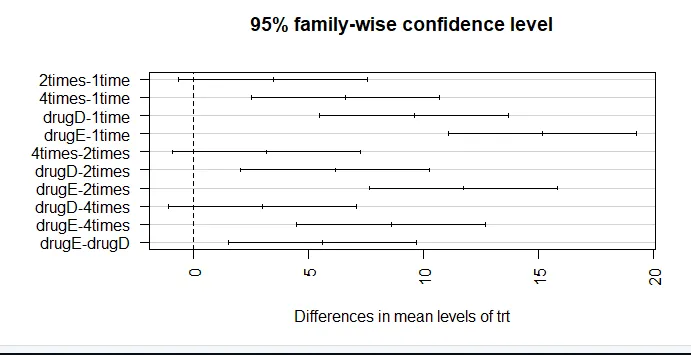
Povprečna znižanja holesterola 1-krat in 2-krat se bistveno ne razlikujejo med seboj (p = 0, 138), medtem ko je razlika med 1-krat in 4-krat bistveno drugačna (p <0, 001).
par (mar = c (5, 8, 4, 2)) # povečanje levega roba zareza (TukeyHSD (aov_model), las = 2)
Zaupanje v rezultate je odvisno od stopnje, v kateri vaši podatki izpolnjujejo predpostavke, na katerih temeljijo statistični testi. Pri enosmerni ANOVA se domneva, da je odvisna spremenljivka običajno porazdeljena in ima v vsaki skupini enako varianco. Za oceno knjižnice predpostavk normalnosti (avtomobila) lahko uporabite QQ ploskev.
QQ zaplet (lm (odziv ~ trt, podatki = holesterol), simulacija = TRUE, main = ”QQ Plot”, oznake = FALSE)
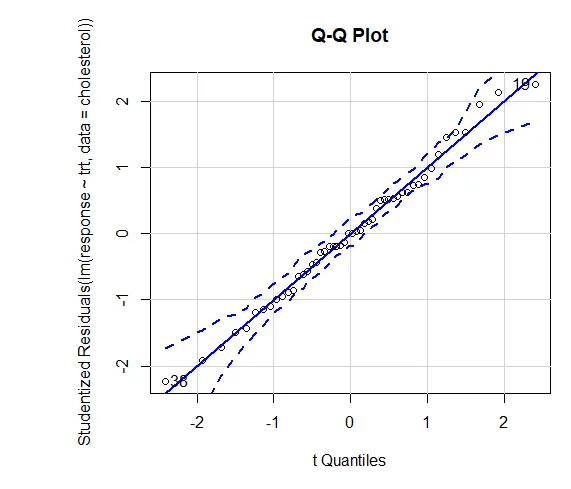
Črtkana črta = 95-odstotna ovojnica zaupanja, kar kaže, da je predpostavka o normalnosti izpolnjena dokaj dobro. ANOVA predpostavlja, da so odstopanja enaka v skupinah ali vzorcih. Za preverjanje te domneve lahko uporabimo Bartlettov test
bartlett.test (odziv ~ trt, podatki = holesterol). Bartlettov test kaže, da se odstopanja v petih skupinah ne razlikujejo bistveno (p = 0, 97).
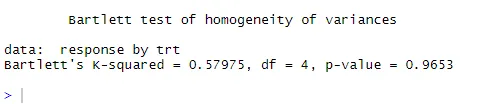
ANOVA je občutljiva tudi na preizkušnjo za odstranjevalce, ki uporabljajo funkcijo outlierTest () v avtomobilskem paketu. Za posodobitev knjižnice avtomobila morda ne bo treba zagnati tega paketa.update.packages(checkBuilt = TRUE)
install.packages("car", dependencies = TRUE)
library(car)
outlierTest(aov_model)
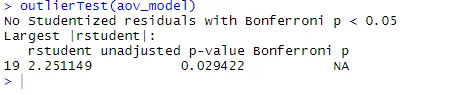
Iz rezultatov lahko vidite, da v podatkih o holesterolu ni odkritosti (NA se pojavi pri p> 1). Če zajamemo QQ, Bartlettov test in zunanji test skupaj, se zdi, da podatki ustrezajo ANOVA modelu.
Dvosmerna Anova
V dvosmerni test ANOVA je dodana še ena spremenljivka. Kadar obstajata dve neodvisni spremenljivki, bomo morali uporabiti dvosmerno ANOVA tehniko in ne enosmerno ANOVA tehniko, ki smo jo uporabili v prejšnjem primeru, ko smo imeli eno stalno odvisno spremenljivko in več kot eno neodvisno spremenljivko. Za preverjanje dvosmerne ANOVA je treba izpolniti več predpostavk.
- Razpoložljivost neodvisnih opazovanj
- Opazovanja je treba normalno razdeliti
- V opazovanjih bi moralo biti odstopanje enako
- Odpadniki ne smejo biti prisotni
- Neodvisne napake
Za preverjanje dvosmerne ANOVA je nabor podatkov dodana druga spremenljivka, imenovana BP. Spremenljivka kaže na stopnjo krvnega tlaka pri bolnikih. Radi bi preverili, ali obstaja bolniška statistična razlika med BP in odmerkom.
df <- read.csv ("datoteka.csv")
df
anova_two_way <- aov (odziv ~ trt + BP, podatki = df)
povzetek (anova_two_way)
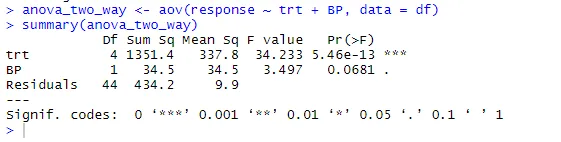
Iz izida je mogoče sklepati, da sta tako trt kot BP statistično različna od 0. Torej je mogoče ničelno hipotezo zavrniti.
Prednosti ANOVA v R
ANOVA test določa razliko v povprečju med dvema ali več neodvisnimi skupinami. Ta tehnika je zelo uporabna za analizo več predmetov, kar je bistveno za analizo trga. S testom ANOVA lahko pridobite potrebne vpoglede v podatke. Na primer med anketo o izdelkih, kjer se od uporabnikov zbira več informacij, kot so nakupovalni seznami, všečke strank in nezadovoljstva. Test ANOVA nam pomaga primerjati skupine prebivalstva. Skupina je lahko moški ali ženska ali različne starostne skupine. ANOVA tehnika pomaga razlikovati med srednjimi vrednostmi različnih skupin prebivalstva, ki so res različne.
Sklep - ANOVA v R
ANOVA je ena najpogosteje uporabljenih metod za testiranje hipotez. V tem članku smo opravili test ANOVA na naboru podatkov, sestavljenem iz petdesetih bolnikov, ki so prejemali zdravljenje z zdravili za zmanjšanje holesterola in nadalje videli, kako je mogoče izvajati dvosmerno ANOVA, če je na voljo dodatna neodvisna spremenljivka.
Priporočeni članki
To je vodnik za ANOVA v R. Tukaj razpravljamo o enosmernem in dvosmernem modelu Anova, skupaj s primeri in prednosti ANOVA. Ogledate si lahko tudi druge naše predlagane članke -
- Regresija proti ANOVA
- Kaj je SPSS?
- Kako razlagati rezultate s testom ANOVA
- Funkcije v R