Excel NORMSINV (kazalo)
- Uvod v program Excel NORMSINV
- Kako uporabljati formulo NORMSINV v Excelu?
Uvod v program Excel NORMSINV
Funkcija obratne normalne kumulativne porazdelitve v excelu je pomembno orodje, ki vrne obratno normalno kumulativno porazdelitev za določeno vrednost verjetnosti, tj. Običajno vrne inverzno normalno normalno kumulativno porazdelitev (ki ima povprečno nič in standardni odklon eno) Funkcija NORM.S.INV je prvič predstavljena v različici Microsoft excel 2010, ki je posodobljena različica funkcije NORMSINV v excelu 2013 in najnovejši različici. Funkcija NORMSINV se večinoma uporablja pri plačilu računov in finančnih analizah.
Sintaksa Excela NORMSINV

Prepir:
Verjetnost - Kar ni nič drugega kot verjetnost, ki ustreza običajni porazdelitvi.
Kako uporabljati formulo NORMSINV v Excelu?
V Microsoftu excel je vgrajena funkcija NORMSINV razvrščena po statistični funkciji, ki je prikazana na spodnjem zaslonu (kjer bo izračunala obratno vrednost običajne kumulativne porazdelitve za določeno verjetnost).
- Pojdite v meni Formule.
- Kliknite Več funkcij, kot je prikazano na spodnjem posnetku zaslona.

- Izberite kategorijo statistike, pod katero bomo našli funkcijo NORM.DIST, kot je prikazano spodaj.
Primer # 1 - Uporaba NORM.DIST in NORMSINV
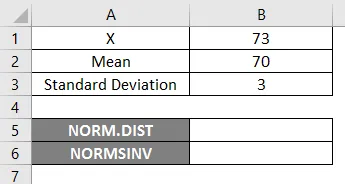
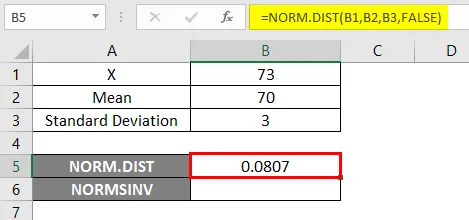
Za uporabo funkcije NORM.DIST začnimo s preprostim primerom, kjer moramo izvedeti ocene študentov, predpostavimo, da imamo razredni izpit s povprečno oceno 70, tj. Mu = 70 in standardni odklon razreda 3 točke, tj. Sigma = 3 tukaj moramo ugotoviti, kakšna je verjetnost, da so študenti dobili ocene 73 ali manj, to je P (X <= 73). Pa si poglejmo, kako ugotoviti verjetnost s funkcijo NORM.DIST.
- X = 3
- Srednja vrednost = 70
- Standardno odstopanje = 3
- Uporabite funkcijo NORM.DIST, kot je spodaj.
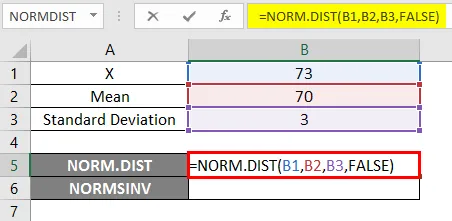
- Če uporabimo zgornjo funkcijo NORM.DIST, bomo dobili verjetnost 0, 0807.
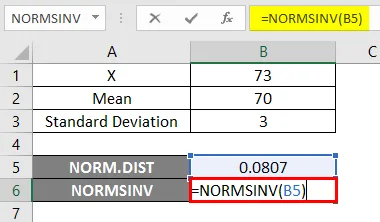
- Zdaj uporabite funkcijo NORMSINV, da ugotovite obratno normalno kumulativno porazdelitev, kot je prikazano spodaj.
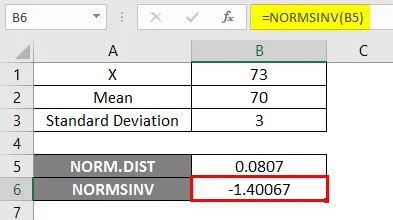
Rezultat -
Na spodnjem rezultatu lahko vidimo, da smo za dano verjetnost dobili negativne vrednosti -1.40067, tj. Obratno od normalne kumulativne porazdelitve.
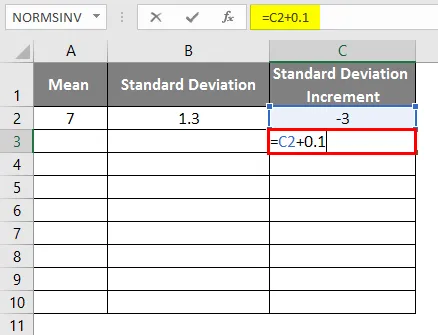
Primer # 2 - Povprečno in natančno standardno odstopanje
Poglejmo še en primer s podatki na osnovi krivulje, da bomo lahko spoznali srednji in natančni standardni odklon.
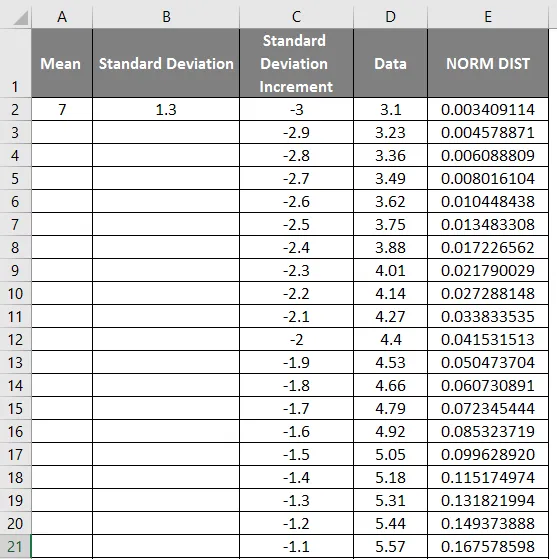
- Srednja vrednost = 7
- Standardno odstopanje = 1, 3
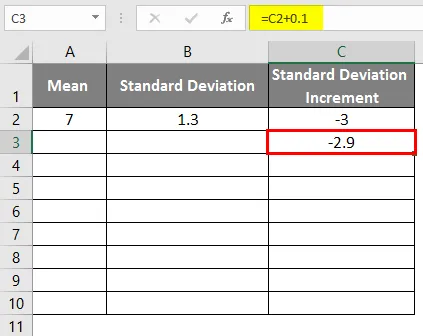
- Standardno povečanje odstopanja kot -3

- Da dobimo krivuljo zvonca, moramo dodati 0, 1 povečanje standardnega odklona, kjer so podatki, kot je prikazano spodaj.
- Po uporabi formule je rezultat prikazan spodaj.
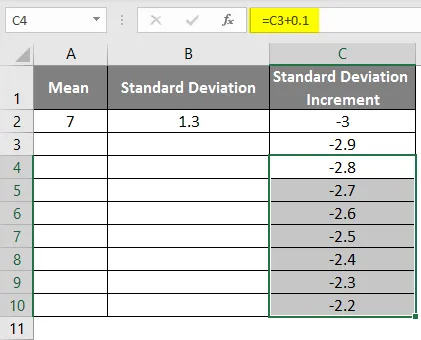
- Povlecite vrednosti, da dobimo več vrednosti, dokler ne dobimo pozitivnih vrednosti, tako da bomo dobili levo krivuljo.
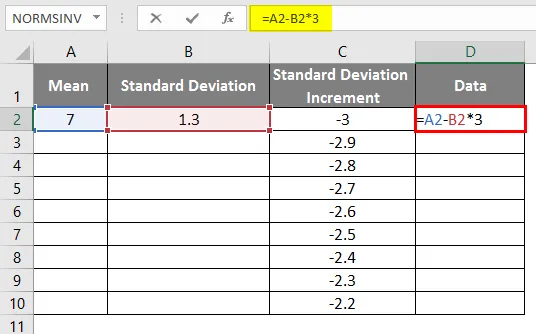
- Da dobimo desno krivuljo, moramo formulo uporabiti kot = povprečni standardni odklon * 3, tako da bomo dobili natančne krivulje.
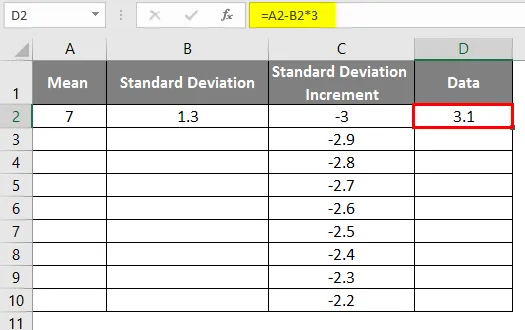
- Po uporabi formule je prikazan spodnji rezultat.
- Kot v zgornjih podatkih za povečanje standardnega odklona, da dobimo levo krivuljo, smo vrednosti povečali za 0, 1
- Isti scenarij se uporablja z uporabo formule kot = 3.1 + STANDARDNO ODDELEK / 10, da dobimo povečanje krivulje 0, 1
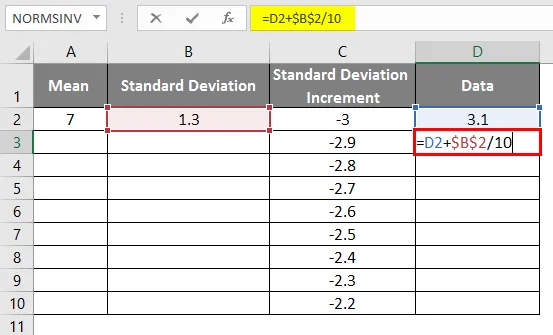
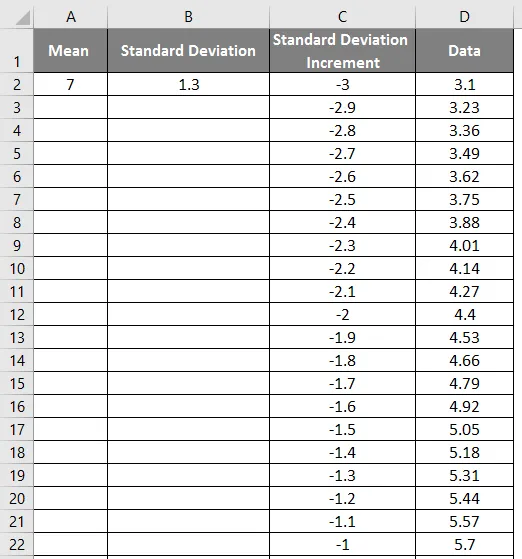
- Po uporabi formule je prikazan spodnji rezultat.

- Povlecite vrednosti, da dobite natančen rezultat, ki je prikazan na spodnjem posnetku zaslona.
- Zdaj uveljavite normalno porazdelitveno funkcijo s formulo = NORM.DIST (vrednost DATA, srednja vrednost, standardni odklon, napačna).
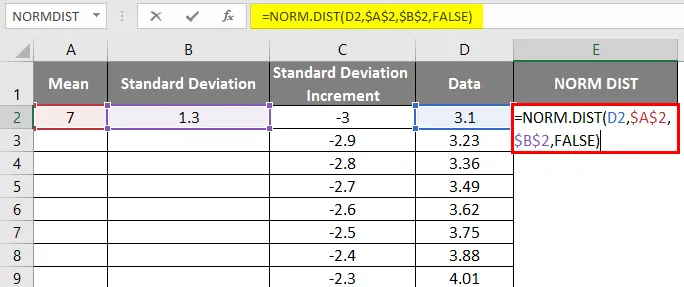
- Spodnji rezultat bomo dobili na naslednji način.
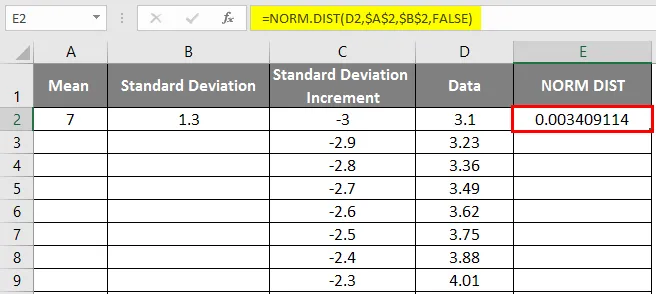
- Povlecite vrednosti, da dobite natančen rezultat, ki je prikazan spodaj.
- Kot lahko vidimo na zgornjem posnetku zaslona, smo izračunali NORMALno porazdelitev od povprečnega in standardnega odklona. Zdaj pa poglejmo, kakšna bo obratna porazdelitev NORMAL z uporabo NORMSINV, ki je prikazan spodaj.
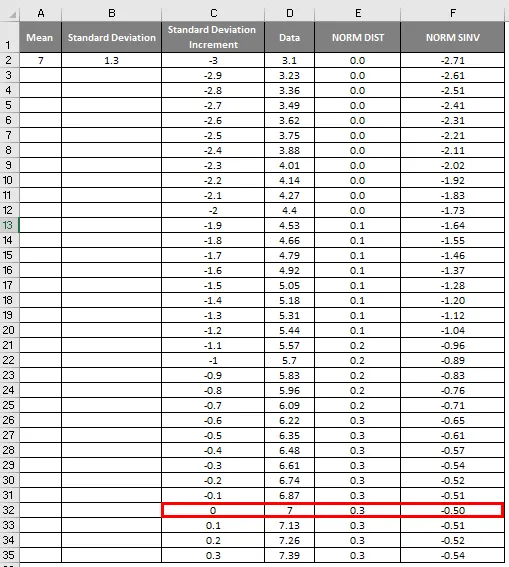
- Tu lahko vidimo, da ima vrednost Zero (0) standardni odklon 7.

Z razpršenim grafom si oglejte levo in desno krivuljo.
- Najprej izberite podatke in stolpec Normal.
- Pojdite na zavihek Vstavljanje in izberite razpršen graf na naslednji način.
- Dobili bomo spodnji graf krivulje, kot je prikazano spodaj.
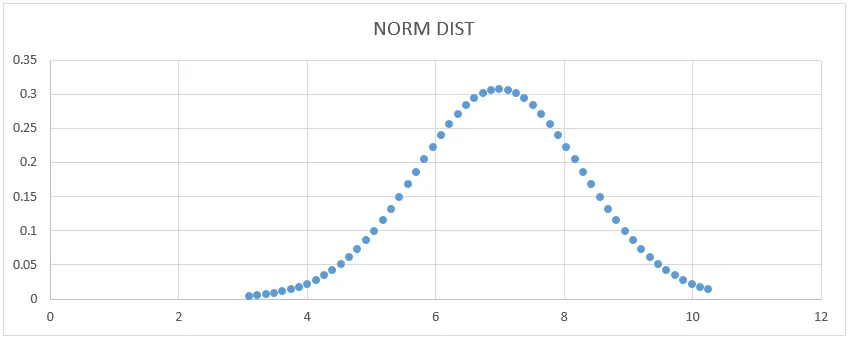
Tu lahko vidimo, da ima srednja vrednost 7 standardno obliko odklona, kjer lahko to pokažemo z risanjem ravne črte, ki jo predstavlja.
- Srednja vrednost = 7
- 1 –Standardno odstopanje označuje 68% podatkov.
- 2 –Standardno odstopanje označuje 95% podatkov.
- 3 –Standardno odstopanje kaže na 99, 7% podatkov.
Graf običajne porazdelitve:
Graf NORMSINV:
Zdaj na zgornji sliki izberite stolpec s podatki in NORM SINV, da dobite spodnji graf, kot sledi.
- Najprej izberite podatke in stolpec Normal.
- Pojdite na zavihek Vstavljanje in izberite razpršeni graf.
- Dobili bomo spodnji graf, ki je prikazan na spodnjem posnetku zaslona.
- Iz zgornjega posnetka zaslona lahko razberemo, da smo dobili natančno obratno vrednost normalne porazdelitve, ki prikazuje isto vrednost, prikazano spodaj.

Primer # 3 - Konfiguriranje leve in desne krivulje
V tem primeru bomo konfigurirali levo in desno krivuljo z uporabo običajne porazdelitvene funkcije. Razmislite o spodnjih podatkih, prikazanih spodaj, kjer ima x negativne vrednosti in se poveča na pozitivne vrednosti.
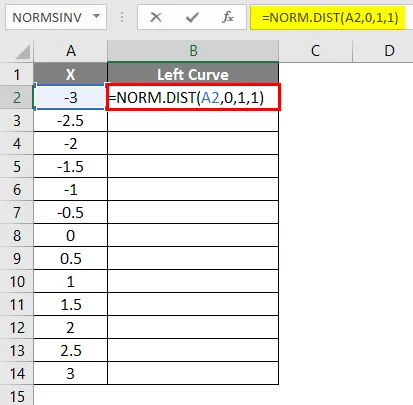
- Uporabi formulo = NORM.DIST (A2, 0, 1, 1).
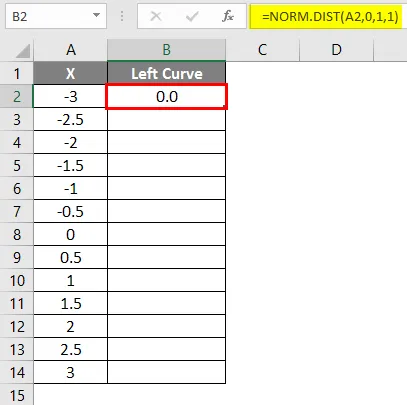
- Po uporabi formule je prikazan spodnji rezultat.
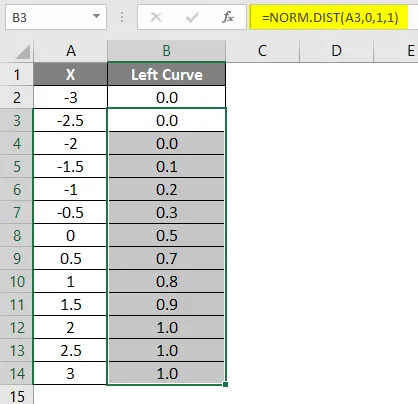
- Povlecite formulo v druge celice.
- Uporabi formulo = 1-B2 .
- Po uporabi formule je rezultat prikazan spodaj.
- V drugo celico povlecite isto formulo.
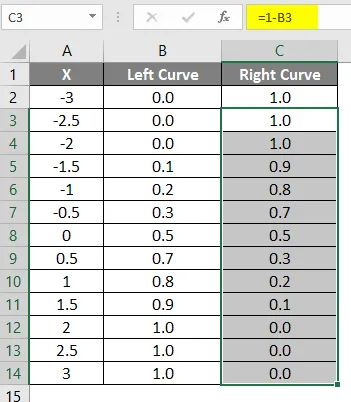
Rezultat zgoraj uporabljene formule je prikazan spodaj.
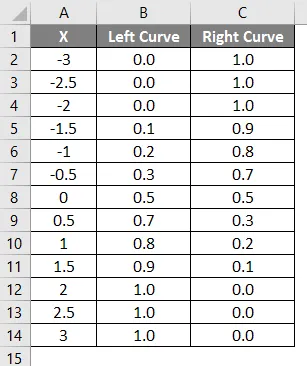
- Vrednosti leve krivulje so bile izračunane z uporabo formule NORMAL DISTRIBUTION z nastavitvijo kumulativne vrednosti kot True in NORMSINV je izračunana s pomočjo leve krivulje.
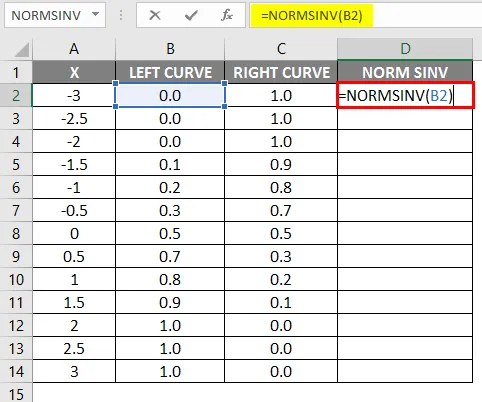
- Po uporabi formule je prikazan spodnji rezultat.
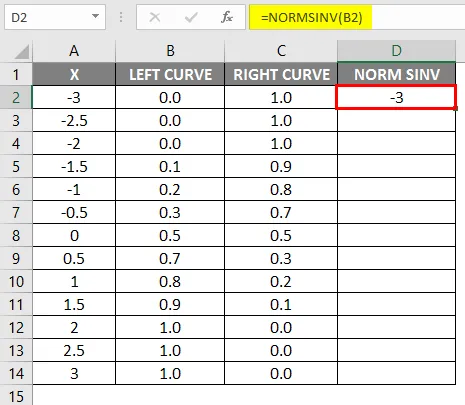
- V drugo celico povlecite isto formulo.
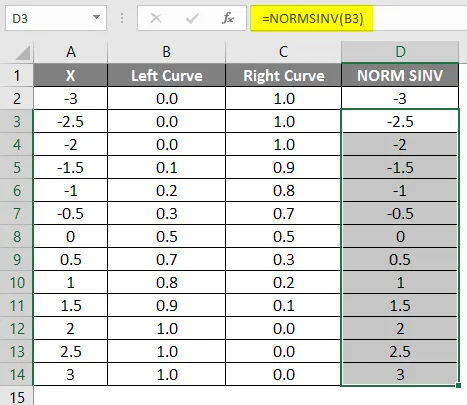
Kot lahko vidimo, da smo za NORMSINV dobili isto vrednost, ki ni nič drugega kot obratna normalna porazdelitev. Na enak način bomo dobili vrednost prave krivulje z izračunom 1-leve vrednosti krivulje. V naslednjem koraku bomo preverili, kako bomo s pomočjo razpršenega grafa dobili višino x.
- Izberite levi stolpec in desni stolpec krivulje.
- Pojdite na vstavitev menija.
- Izberite razpršeni graf na naslednji način.
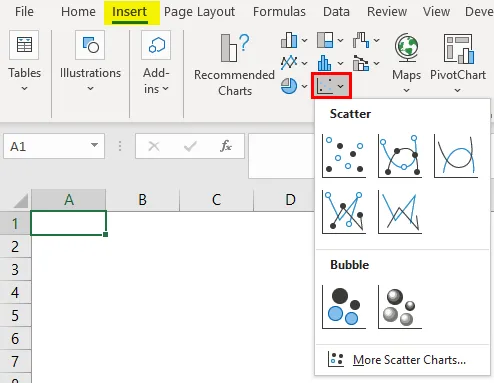
Dobili bomo spodnji rezultat grafa, kot je prikazano spodaj.
NORM SINV Graf:
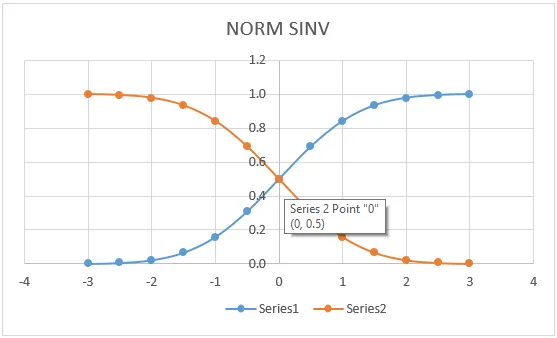
Na spodnjem grafu lahko vidimo, da ima leva leva krivulja vrednosti NORM DISTRIBUTION natančno ujemanje za (0, 0, 5), ki leži na sredini črte, kjer bomo dobili isti graf, če se prijavimo za NORMDIST.
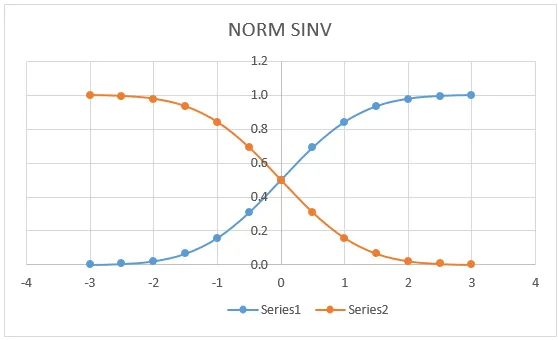
Tu na zgornjem grafu je zelo jasno razvidno, da smo dobili točno srednjo vrednost v središčni točki, ki označuje:
- X = 0
- Leva krivulja = 0, 5
- Desna krivulja = 0, 5
Prikazali smo ga za ogled vrednosti NORMSINV v grafični obliki, kot je prikazano spodaj.
Spomniti se o Excelu NORMSINV
- # vrednost! Do napake pride, kadar je navedeni argument neštevilčna ali logična vrednost.
- V funkciji normalne distribucije običajno dobimo #NUM! napaka zaradi argumenta standardnega odklona je manjša ali enaka nič.
Priporočeni članki
To je vodnik za Excel NORMSINV. Tukaj razpravljamo o uporabi NORMSINV v Excelu skupaj s praktičnimi primeri in prenosno predlogo Excela. Ogledate si lahko tudi druge naše predlagane članke -
- Kako uporabljati imenik v Excelu?
- Delo z Matrix v Excelu
- Kaj če analiza v Excelu
- Formula NPV v Excelu