Kompleksne številke v MATLAB - Kako ustvariti kompleksno številko?

Uvod v zapletene številke v MATLAB

Kompleksne številke so kombinacija resničnih števil in namišljenih števil v obliki p + qi, kjer sta p in q realna števila in i je namišljeno število. Določeno je namišljeno število, kjer je i rezultat enačbe a 2 = -1. Za označevanje namišljenih enot lahko uporabimo i ali j. Ker se pri vseh matematičnih izračunih uporabljajo kompleksna števila, se Matlab uporablja predvsem za izvajanje matematičnih izračunov. Torej, kompleksna števila so pomemben del učenja Matlaba.

Generacija kompleksnih števil v MATLAB

Kompleksne številke lahko v Matlabu ustvarite ali deklarirate s pomočjo funkcije 'kompleks'. Zapletene številke lahko ustvarimo tudi tako, da poiščemo kvadratni koren katerega koli negativnega števila. V Matlabu lahko s i ali j označimo namišljeni del kompleksnega števila.

Primeri

X = 4 + 5i

Tu je X kompleksna številka, ki vsebuje 2 dela, tj stvarni in namišljeni del. 4 je resnični del in 5 je namišljeni del. Prave in namišljene dele lahko s pomočjo funkcij v Matlabu najdemo.

a = real (X) = 4 (To daje dejanski del kompleksnega števila)
b = imag (X) = 5 (To daje namišljeni del kompleksnega števila)
kompleks (6, 7) = 6 + 7i (Ta funkcija se uporablja za ustvarjanje kompleksnega števila)

V Matlabu lahko ustvarimo tudi zapletene matrike, ki jih lahko razglasimo tudi s pomočjo kompleksnih funkcij.

a = zapleteno (x, y)

Za x in y obstajajo določeni pogoji, ki bi jim morali slediti kot x in y ne bi smeli biti enojni ali dvojni. Zapleten skalar lahko ustvarite, če sta dva vhoda skalarne narave, kot npr.

X = kompleksno (5, 3)
X = 5.0000 + 3.0000i

Podobno lahko ustvarimo zapleten vektor, če imamo kot vektorje dva vhoda.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = zapleteno (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Ustvarimo lahko kompleksno številko, ki ima samo enega skalarja,

X = kompleksno (10)
X = 10, 0000 + 0, 0000i

Obstajajo določeni pogoji, ki bi jim morali slediti vhodni in izhodni argumenti,

Vhodni argumenti vsebujejo resnične in namišljene dele, kot je x kateri y. x in y bi morali biti v MATLAB skalarni, vektorski, večdimenzionalni niz ali matrika. x in y morata biti enaka. Morali bi biti iste vrste podatkov, vendar je nekaj izjem, kot je dvojna, ki se lahko uporablja z enojnim, celo število pa je mogoče kombinirati z dvojnikom, ki je skalarno.

Izhod matrike je lahko vektorski, skalarni, matrični ali večdimenzionalni niz, odvisno od vhodnih argumentov. Velikost izhoda naj bo enaka vhodu. Če so vhodni argumenti različnih podatkovnih vrst, potem izhodni podatek določa,

Če je kateri koli od vhodnih argumentov enotnega značaja, potem bi moral biti tudi rezultat enak.
Če je kateri koli od vhodnih argumentov po naravi celo število, bi moral biti izhod celoten podatkovni tip.

S pomočjo izrealne funkcije lahko preverimo, ali je matrika resnična ali namišljena.

Koda:

X = (2+i, 1); Isreal(X)

Izhod:

Koda:

Isreal (X (2))

Izhod:

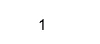
Za ekstrahiranje resničnih in namišljenih delov lahko v Matlabu uporabimo resnične in slikovne funkcije,

Koda:

real(X)

Izhod:

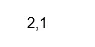
Koda:

imag(X)

Izhod:

Delovanje in funkcije zapletenih števil v MATLAB

V Matlabu je več operacij in funkcij, ki jih je mogoče izvesti s pomočjo kompleksnih števil

abs: Ta funkcija se uporablja za iskanje modula katerega koli kompleksnega števila v obliki p + qi. abs (2 + 3i) = kvadratni koren (2 2 + 3 2) = (13) 0, 5
kot: za iskanje faznega kota kompleksnega števila.

Obstajajo določeni nasveti, ki jih je treba upoštevati za pravilno delovanje kompleksnih števil v Matlabu, kot npr.

Izogibajmo se uporabi i in j kot del imen spremenljivk, ki se uporabljajo pri označevanju namišljenih delov kompleksnega števila.
Izogibajmo se uporabi j ali i, če je namišljeni del 1. Namesto tega lahko uporabimo 1j ali 1i.
V Matlabu lahko ustvarimo kompleksno funkcijo, kadar i in j na nekem delu uporabljamo kot imena spremenljivk, vhodni argumenti niso enojnega ali dvojnega tipa in namišljeni del je nič.

Zaključek

Kompleksne številke se uporabljajo na matematičnem ali inženirskem področju. Številne resnične ali praktične aplikacije je mogoče opisati z namišljenim delom kompleksnih števil. Zato je razumevanje uporabe in uporabe kompleksnih števil na različnih platformah pomembno, zlasti če imate opravka s katero koli fizično ali matematično domeno.

Priporočeni članki

To je vodnik za zapletene številke v MATLAB. Tukaj razpravljamo o uvedbi in nastanku kompleksnih števil v matlabu, vključno z njegovimi primeri delovanja in funkcije. Če želite izvedeti več, si oglejte tudi naslednje članke -